Этот материал будет сильно полезен студентам, которым требуется написать программу вычисления определенного интеграла методом левых прямоугольников.
Рассмотрим метод левых прямоугольников в общем виде. Допустим, задана некоторая функция $y = f(x)$. И необходимо найти следующий определенный интеграл: $\int\limits_a^b f(x)\ dx$.
Геометрически имеем следующую картину (рис. 1)
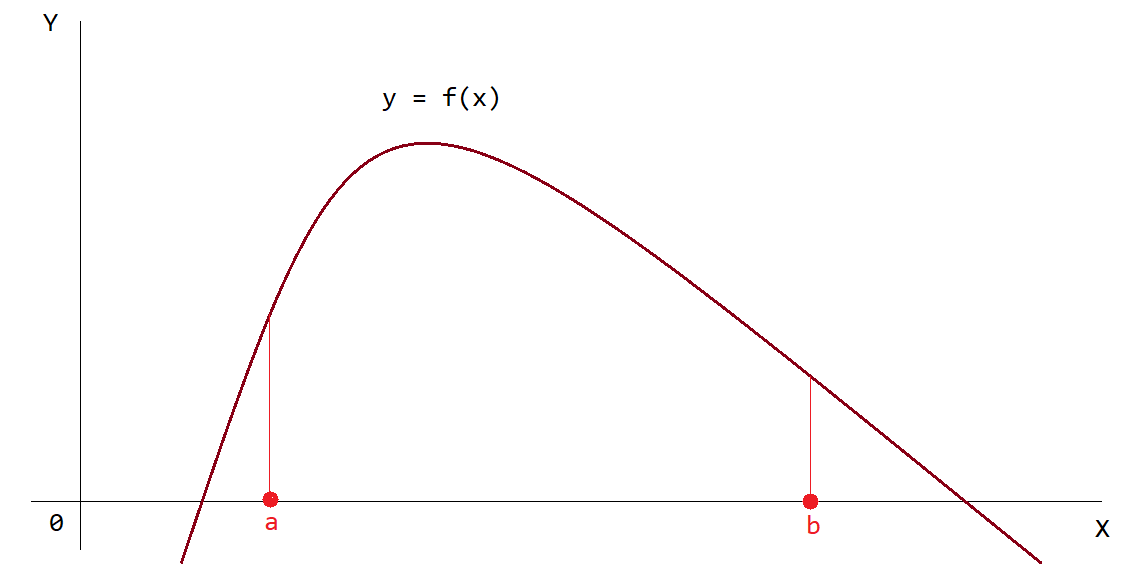
Рисунок 1 — График функции $y = f(x)$ в общем виде
Как известно, значение определенного интеграла равно площади криволинейной трапеции (рис. 2).
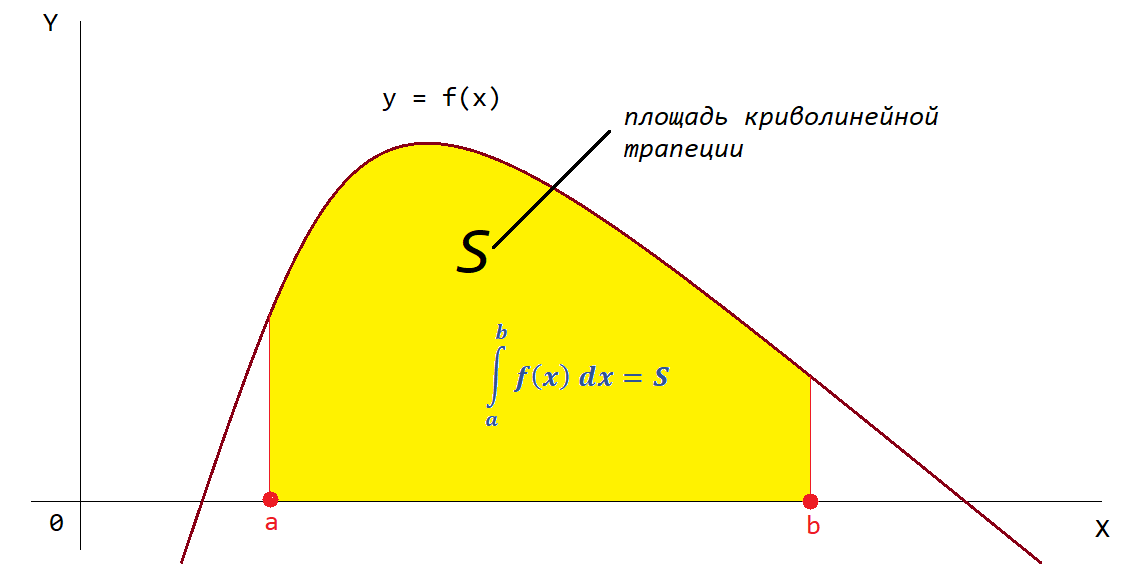
Рисунок 2 — Значение определенного интеграла равно площади криволинейной трапеции
Разобьем отрезок интегрирования $[a;\ b]$ на $n$ равных отрезков. Для демонстрации метода левых прямоугольников я возьму совсем небольшое значение $n = 5$. Хотя на практике чем больше число разбиений отрезка $[a;\ b]$, тем лучше, так как получается более точное приближенное значение заданного определенного интеграла (рис. 3).
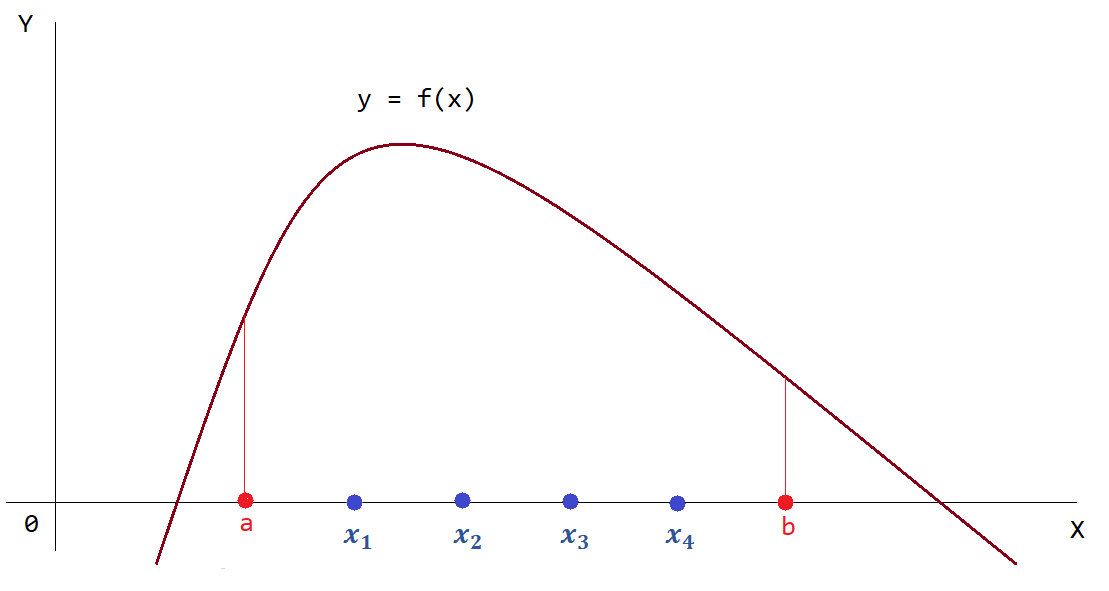
Рисунок 3 — Разбиение отрезка [a; b] на 5 равных частей/отрезков
Затем из точек $x_1,\ x_2,\, x_3,\, x_4$ проведем перпендикуляры до пересечения с графиком функции $y = f(x)$ (рис. 4).
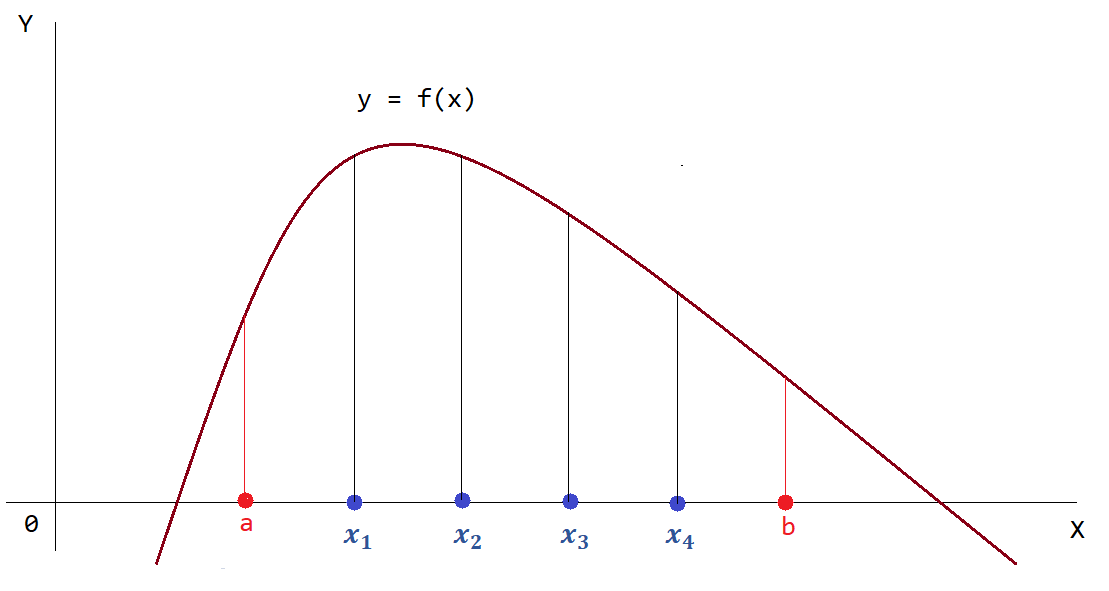
Рисунок 4 — Построение перпендикуляров из концов всех отрезков разбиения
Проведем построение левых прямоугольников. Почему именно левых? Потому что построение прямоугольников будем вести слева направо, получая сторону прямоугольника из точки, соответствующей левому значению функции $y = f(x)$ (рис. 5).
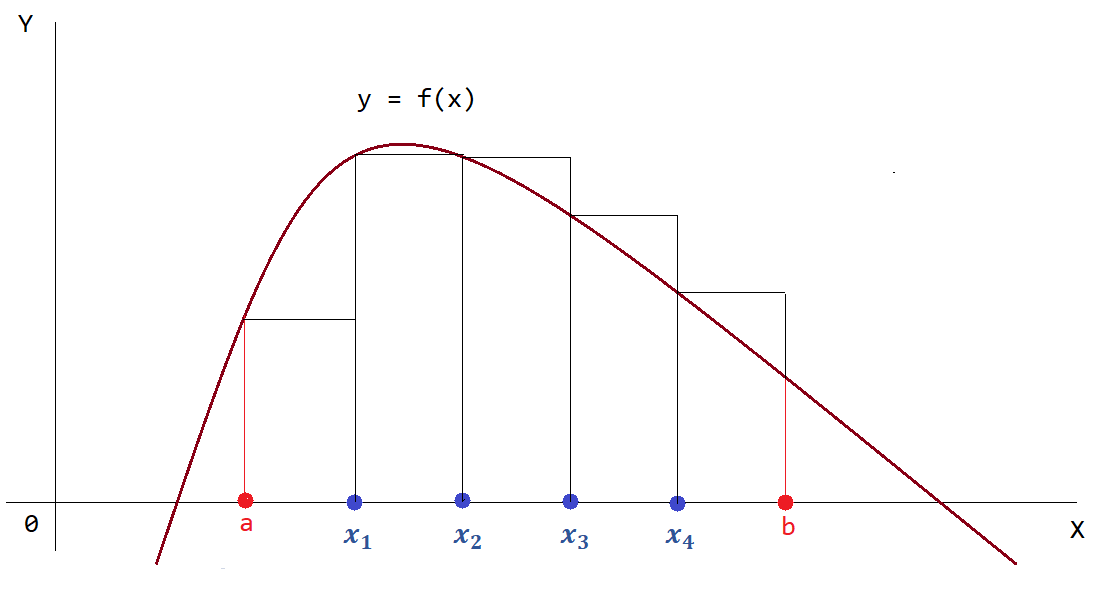
Рисунок 5 — Построение левых прямоугольников
Так как изначально отрезок интегрирования $[a;\ b]$ был разбит на $5$ равных частей ($n = 5$), то у нас образовалось также $5$ неодинаковых по площади прямоугольников (рис. 6).
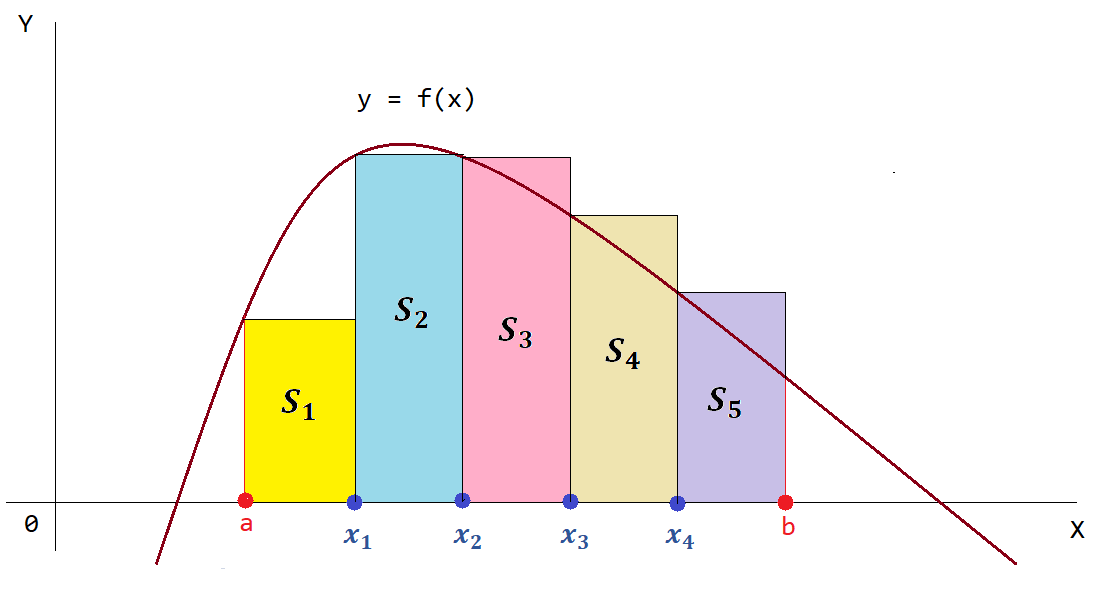
Рисунок 6 — Обозначение площадей образованных левых прямоугольников
Получается, что значение заданного определенного интеграла равно сумме площадей этих прямоугольников, то есть справедливо следующее равенство: $$\int\limits_a^b f(x)\ dx = S_1 + S_2 + S_3 + S_4 + S_5$$.
Заметьте, что ширина всех этих $5$ прямоугольников одинаковая и вычисляется по формуле
$h = \frac{b\ -\ a}{n}$, где
$a,\ b$ — границы интегрирования;
$n$ — количество разбиений отрезка $[a;\ b]$.
Относительно длин/высот этих прямоугольников эти значения равны значениям анализируемой функции $y = f(x)$ в концах отрезков разбиения.
💡 И вот наша конечная цель — написать программу, а если быть более точным, закодировать программную функцию, которая на вход принимает следующие параметры:
- указатель на заданную функцию, которая подвергается интегрированию;
- границы отрезка интегрирования ($a,\ b$);
- количество разбиений отрезка интегрирования ($n$).
И в качестве результата эта функция вернет приближенное значение интересуемого нас определенного интеграла с какой-то точностью.
Ранее мы записали формулу для вычисления определенного интеграла через сумму площадей $5$ прямоугольников, но в теории численного интегрирования существует общая формула для таких вычислений. Если принять, что левая граница интегрирования $a = x_0$, то эта формула примет вид:
$$\int\limits_a^b f(x)\ dx \approx \sum\limits_{i=0}^{n-1}f(x_i)(x_{i+1}\ -\ x_i)$$
В этой формуле разность $(x_{i+1}\ -\ x_i)$ есть ничто иное, как ширина левых прямоугольников ($h$). При этом это значение положительное, так как из большего ($x_{i+1}$) вычитается меньшее ($x_i$). Поэтому формулу можно переписать так:
$$\int\limits_a^b f(x)\ dx \approx \sum\limits_{i=0}^{n-1}f(x_i)\cdot h \approx h \cdot \sum\limits_{i=0}^{n-1}f(x_i)$$
Давайте сейчас разберем конкретный пример. Решим его математически и напишем программу на языке «чистый» Си (стандарт C89).
➡ Например, требуется найти значение определенного интеграла $\int\limits_1^5 (-x^2 + 6x + 7)\ dx$.
Изобразим график заданной функции $f(x) = -x^2 + 6x + 7$ на отрезке $[-2;\ 8]$ (рис. 7).
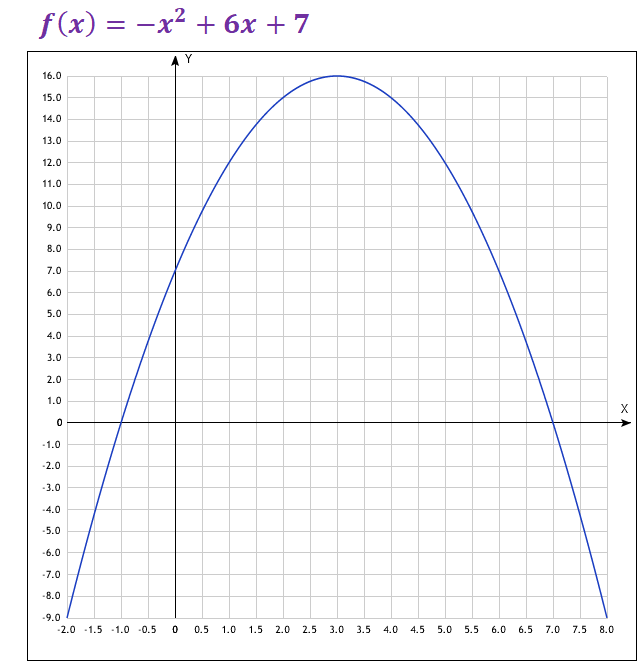
Рисунок 7 — График функции $f(x) = -x^2 + 6x + 7$
Как мы выяснили ранее, значение определенного интеграла равно площади криволинейной трапеции (рис. 8).
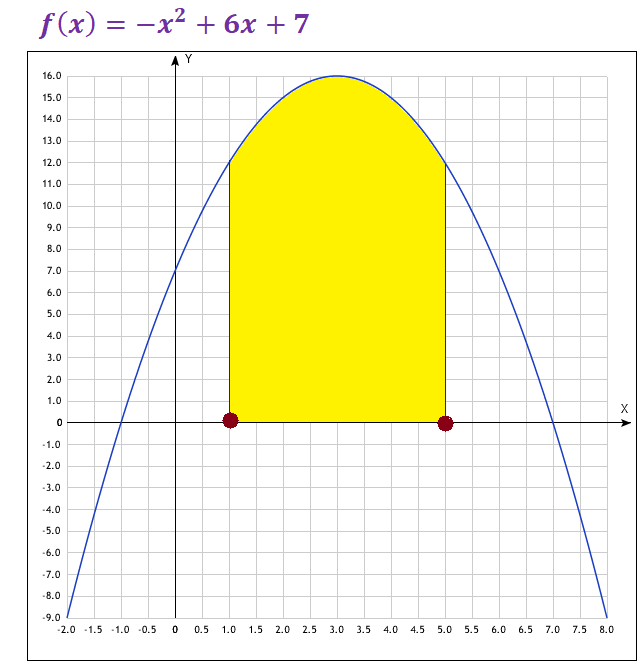
Рисунок 8 — Желтым цветом выделена площадь криволинейной трапеции
С точки зрения математики, такая задача решается по формуле Ньютона-Лейбница. Рассмотрим функцию $f(x) = -x^2 + 6x + 7$ и найдем ее первообразную $\rightarrow$ $F(x) = -\frac{x^3}{3} + 3x^2 + 7x$.
$F(5) = -\frac{125}{3} + 3 \cdot 25 + 7 \cdot 5 = -\frac{125}{3} + 110$
$F(1) = -\frac{1}{3} + 3 + 7 = -\frac{1}{3} + 10$
$\int\limits_1^5 (-x^2 + 6x + 7)\ dx = F(5)\ -\ F(1) = -\frac{125}{3} + 110\ -\ (-\frac{1}{3} + 10) = 58.666667$
Поскольку наша конечная цель — создать программную функцию, приближенно вычисляющую значение определенного интеграла, то мы подошли к одному из ответственнейших моментов статьи. Внимательно познакомьтесь со следующим кодом программы, в котором запрограммирован метод левых прямоугольников.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
#include <stdio.h> #include <math.h> #include <locale.h> #include <conio.h> #include <Windows.h> // непрерывная функция f(x) = -x^2 + 6x + 7, которая подвергается интегрированию на отрезке double F(const double px) { return (-pow(px, 2) + 6 * px + 7); } // метод левых прямоугольников (вычисление определенного интеграла) double LeftSquares(double (*pfunc)(const double), const double pa, const double pb, const unsigned int pn) { double square; // хранит приближенное значение определенного интеграла double h; // шаг табулирования (ширина прямоугольников) unsigned int i; // счетчик цикла (количество прямоугольников) // вычисляем шаг интегрирования h = (pb - pa) / pn; square = 0.0; // просматриваем весь отрезок интегрирования for(i = 0; i < pn; i++) square += pfunc(pa + i * h); // вычисляем значение функции в заданной точке square *= h; // получаем окончательный ответ // в качестве ответа функция возвращает приближенное значение определенного интеграла return square; } int main(void) { double a, b; // границы интегрирования unsigned int n; // количество разбиений отрезка интегрирования double (*func)(const double); // указатель на функцию с одним вещественным константным аргументом // настройка заголовка консольного окна программы static const TCHAR* title = TEXT("Метод левых прямоугольников"); SetConsoleTitle(title); setlocale(LC_ALL, ""); // русификация диалогов программы // ввод с клавиатуры границ интегрирования и количества разбиений отрезка интегрирования printf("Введите левую границу интегрирования(a): "); scanf("%lf", &a); printf("Введите правую границу интегрирования(b, b > a): "); scanf("%lf", &b); printf("Введите количество разбиений отрезка интегрирования (n - натуральное число): "); scanf("%u", &n); func = F; // ставим указатель-функцию на функцию F // выводим приближенное значение определенного интеграла с точностью до миллионных printf("Значение определенного интеграла (метод левых прямоугольников): %0.6lf", LeftSquares(func, a, b, n)); printf("\n\nДля завершения работы программы нажмите ENTER..."); getch(); // задержка работы программы, чтобы была возможность просмотреть результат return 0; // передача управления в ОС (официальное закрытие работы программы) } |
При работе программы границы интегрирования и количество разбиений отрезка интегрирования вводятся с клавиатуры. В роли подынтегральной функции выступает $f(x) = -x^2 + 6x + 7$.
По условию задачи $a = 1,\ b = 5$, то эти же значения и будем вводить с клавиатуры. А что делать с количеством разбиений отрезка интегрирования? Хороший вопрос! К его обсуждению мы вернемся позже, а сначала давайте введем небольшое значение, например $n = 5$. Тогда получим следующие результаты:
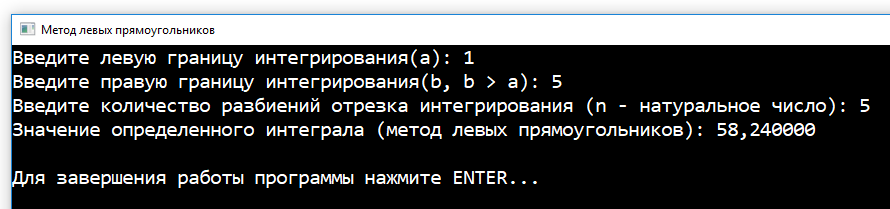
Рисунок 9 — Результаты работы программы ($n = 5$)
💡 Давайте сравним результаты, полученные «чистой» математикой, когда задействовали формулу Ньютона-Лейбница, с программным ответом.
Формула Ньютона-Лейбница: $58.666667$
Результаты программы: $58.240000$.
Все расчеты мы производим до $6$-го знака после запятой, то есть до миллионных.
Очевидно, что формула Ньютона-Лейбница дает эталонный ответ, а программа — приближенный. Погрешность расчетов программы составила $|58.666667 — 58.240000| = 0.426667$. На самом деле, это чудовищная погрешность! 🙂
Дело в том, что мы задали в программе слишком малое количество разбиений($n$). Давайте протестируем программу, задав $n = {10, 25, 100, 500}$.
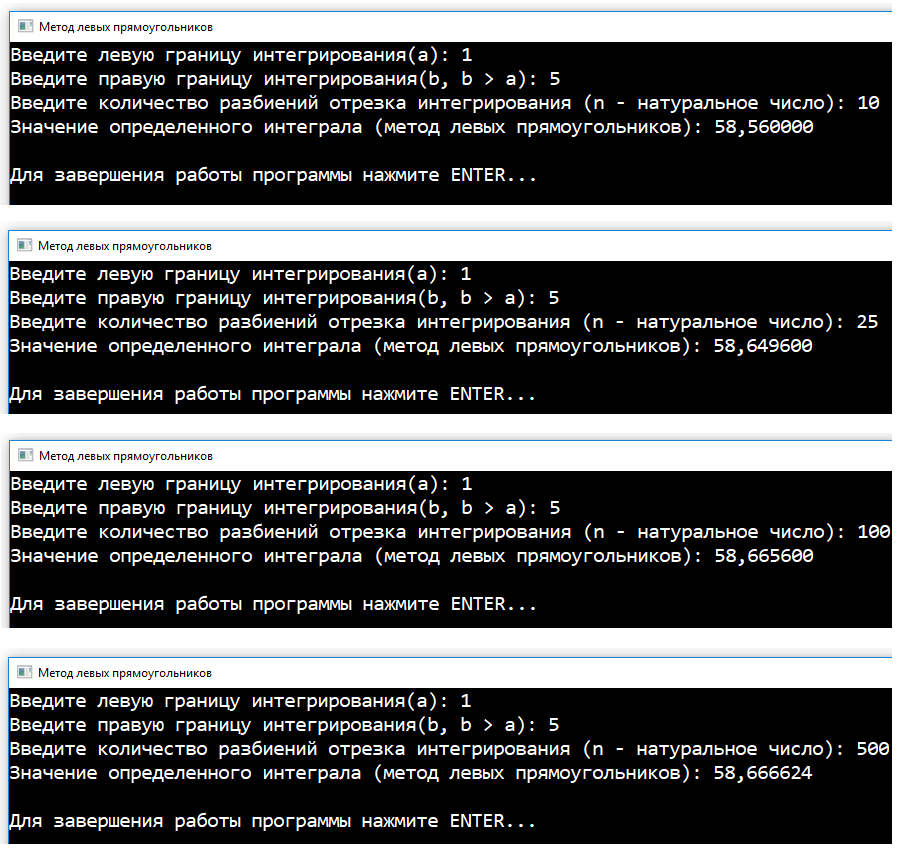
Рисунок 10 — Результаты работы программы при n = {10, 25, 100, 500}
Однозначно, чем больше $n$ (количество разбиений отрезка интегрирования), тем точнее получается расчет.
Давайте сведем в таблицу тесты при разных количествах разбиений ($n$) и для каждого программного результата определим абсолютную погрешность.
Эталонное значение интеграла $\int\limits_1^5 (-x^2 + 6x + 7)\ dx$ составляет $58.666667$.
| № | $n$ | Результаты программы | Погрешность программного результата |
| $1$ | $5$ | $58.240000$ | $0.426667$ |
| $2$ |
$10$ |
$58.560000$ |
$0.106667$ |
| $3$ |
$25$ |
$58.649600$ |
$0.017067$ |
| $4$ |
$100$ |
$58.665600$ |
$0.001067$ |
| $5$ |
$500$ |
$58.666624$ |
$0.000043$ |
| $6$ |
$750$ |
$58.666648$ |
$0.000019$ |
| $7$ |
$1000$ |
$58.666656$ |
$0.000017$ |
| $8$ |
$3500$ |
$58.666666$ |
$0.000001$ |
| $9$ |
$8400$ |
$58.666667$ |
$0.000000$ |
Чтобы достичь точности $EPS = 0.000001$, требуется разбивать отрезок интегрирования $[1;\ 5]$ ориентировочно на $8000+$ равных частей.
Выше я привел пример программы (на языке «чистый» Си, стандарт С89), которая по заданным границам отрезка интегрирования и количеству разбиений приближенно вычисляет значение заданного определенного интеграла. Но в вузах от студентов требуют, чтобы они написали программу, вычисляющую определенный интеграл с заданной точностью! И, например, сообщают, что нужна точность вычислений до одной десятитысячной или одной миллионной и т.п.
Для такого случая вводить с клавиатуры $n$ (количество разбиений) уже не требуется. Достаточно знать аналитический вид подынтегральной функции, а также задать границы интегрирования ($a$ и $b$).
Возникает интересный вопрос: а какое количество разбиений ($n$) надо использовать в программе? Если взять небольшое $n$, то велика вероятность, что мы не добьемся заданной точности. Если взять сумасшедше большое значение $n$, то программа может слишком долго выполняться, и будет перевыполнен результат по точности, то есть легко расчеты могут «улететь» в точность, равную одной миллиардной или даже точнее.
💡 Необходимо применить правилом Рунге. Это правило оценивает погрешность численных методов.
Основная идея следующая. Сначала вычисляется значение определенного интеграла($I_n$) для стартового $n$. Затем $n$ удваивается ($n \rightarrow 2n$), и снова повторяется расчет определенного интеграла($I_{2n}$). Затем вычисляется погрешность по формуле: $\Delta_{2n} = \frac{1}{3}|I_{2n} — I_n|$.
В итоге если выполняется следующее неравенство $\Delta_{2n} < EPS$, где
$EPS$ — заданная точность, то вычисления прекращаются, и считаем, что наши расчеты достигли заданной точности!
Если неравенство ложно, то увеличиваем вдвое количество разбиений: $2n \rightarrow 4n \rightarrow 8n \rightarrow 16n \rightarrow …$ В результате мы все равно достигнем заданной точности! Возможно, для этого придется оперировать миллионами разбиений отрезка интегрирования $[a;\ b]$.
Хорошо, а от какого первоначального значения $n$ стоит «танцевать»? На какое число равных отрезков надо разбить заданный отрезок интегрирования на самом старте? Здесь нет однозначного ответа — надо смотреть на точность. Если нужна небольшая точность, допустим, до «одной сотой», то стартовать можно от $n = 10$. Если нужна точность до «одной миллиардной», то можно задавать $n = 1\ 000$.
Немного изменим условие задачи, которую мы решали чуть раньше.
Найти значение определенного интеграла $\int\limits_1^5 (-x^2 + 6x + 7)\ dx$ с точностью $EPS = 0.0001$.
Теперь с клавиатуры мы будем вводить только границы отрезка интегрирования и больше ничего. Используя правило Рунге, мы постепенно добьемся заданной погрешности в расчетах.
Примечание. Вы скажете, а зачем нам вводить границы отрезка интегрирования, ведь нам эти значения заданы по условию задачи?! Да, верно. Но мы же пишем программу, разрабатываем алгоритм, а алгоритм должен быть массовым, то есть правильно работать при любых допустимых входных данных. Также получаем дополнительную гибкость. Ведь мы сможем тестировать программу на любых введенных с клавиатуры значениях.
В итоге у меня получилась следующая программа, написанная на языке «чистый» Си (стандарт С89):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
#include <stdio.h> #include <math.h> #include <locale.h> #include <conio.h> #include <Windows.h> // непрерывная функция f(x) = -x^2 + 6x + 7, которая подвергается интегрированию на отрезке double F(const double px) { return (-pow(px, 2) + 6 * px + 7); } // метод левых прямоугольников (вычисление определенного интеграла) double LeftSquares(double (*pfunc)(const double), const double pa, const double pb, const unsigned int pn) { double square; // хранит приближенное значение определенного интеграла double h; // шаг табулирования (ширина прямоугольников) unsigned int i; // счетчик цикла (количество прямоугольников) // вычисляем шаг интегрировавания h = (pb - pa) / pn; square = 0.0; // просматриваем весь отрезко интегрирования for(i = 0; i < pn; i++) square += pfunc(pa + i * h); // вычисляем значение функции в заданной точке square *= h; // получаем окончательный ответ // в качестве ответа функция возвращает приближенное значение определенного интеграла return square; } int main(void) { #define EPS 0.0001 // точность вычислений (одна десятитысячная) double a, b; // границы интегрирования unsigned int n; // количество разбиений отрезка интегрирования double (*func)(const double); // указатель на функцию с одним вещественным константным аргументом double I1, I2; // значение определенного интеграла (когда n = i, n = 2i) // настройка заголовка консольного окна программы static const TCHAR* title = TEXT("Метод левых прямоугольников"); SetConsoleTitle(title); setlocale(LC_ALL, ""); // русификация диалогов программы // ввод с клавиатуры границ интегрирования printf("Введите левую границу интегрирования(a): "); scanf("%lf", &a); printf("Введите правую границу интегрирования(b, b > a): "); scanf("%lf", &b); n = 10; // стартовое количество разбиений отрезка интегрирования func = F; // ставим указатель-функцию на функцию F // считаем значение определенного интеграла для n1 = 10 I1 = LeftSquares(func, a, b, n); n *= 2; // увеличиваем вдвое количество разбиений // считаем значение определенного интеграла для n2 = 20 (2n1) I2 = LeftSquares(func, a, b, n); // используем правило Рунге для достижения заданной точности (EPS = 0.0001) while(1.0/3.0 * fabs(I2 - I1) >= EPS) { I1 = I2; n *= 2; // на каждой итерации количество разбиений увеличивается вдвое I2 = LeftSquares(func, a, b, n); } // выводим приближенное значение определенного интеграла с точностью до статысячных printf("Значение определенного интеграла (метод левых прямоугольников): %0.5lf", I2); printf("\n\nДля завершения работы программы нажмите ENTER..."); getch(); // задержка работы программы, чтобы была возможность просмотреть результат return 0; // передача управления в ОС (официальное закрытие работы программы) } |
При запуске программы вводим такие границы интегрирования ($a = 1,\ b = 5$) и получаем следующий результат:
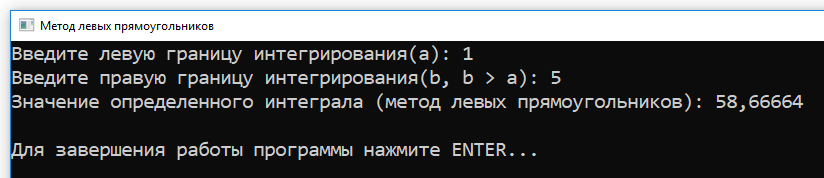
Рисунок 11 — Вычисление определенного интеграла с заданной точностью ($EPS = 0.0001$)
Для проверки корректности полученного программного приближенного результата необходимо сравнить его с эталонным значением (вычисляется по формуле Ньютона-Лейбница).
Формула Ньютона-Лейбница: $58.66667$.
Результат программы: $58.66664$.
Погрешность расчетов программы составила $|58.66667 — 58.66664| = 0.00003$. Полученная погрешность меньше, чем заданная точность ($EPS = 0.0001$), следовательно, все требования в постановке задачи успешно реализованы.
На старте $EPS = 0.0001,\ a = 1,\ b = 5,\ n = 10$.
| $I_n$ | $I_{2n}$ | $\Delta_{2n} \approx |I_{2n} — I_n|$ | $\Delta_{2n} < EPS$ |
| $58.56000 (n = 10)$ | $58.64000 (n = 20)$ | $0.08$ | false |
| $58.64000 (n = 20)$ | $58.66000 (n = 40)$ | $0.02$ | false |
| $58.66000 (n = 40)$ | $58.66500 (n = 80)$ |
$0.005$ |
false |
| $58.66500 (n = 80)$ | $58.66625 (n = 160)$ |
$0.00125$ |
false |
| $58.66625 (n = 160)$ | $58.66657 (n = 320)$ |
$0.00032$ |
false |
| $58.66657 (n = 320)$ | $58.66664 (n = 640)$ |
$0.00007$ |
true |
Из данных таблицы видно, чтобы достигнуть заданной точности вычислений ($EPS = 0.0001$) пришлось разбить заданный отрезок интегрирования $[1;\ 5]$ на $640$ равных частей.
➡ Возможно, у многих читателей этого материала в голове крутится вопрос: «А зачем вообще что-то здесь программировать? Ведь есть эталонная математическая формула Ньютона-Лейбница, которая рассчитает значение определенного интеграла с заданной точностью!».
Во-первых, чтобы использовать формулу Ньютона-Лейбница, надо взять первообразную подынтегральной функции. Это нужно уметь делать.
Во-вторых, не для каждой подынтегральной функции можно получить первообразную. И это главный факт, из-за которого надо использовать приближенные способы вычисления определенного интеграла. Как раз таки метод левых прямоугольников приближенно вычисляет такое значение.
Например, попробуйте найти первообразную для этой функции $g(x) = e^{\sqrt{x}} \cdot \sin(x)$, используя классические формулы и преобразования. Вот и все, приехали.
Если условие задачи звучит так — найти значение определенного интеграла $\int\limits_{-2}^{8.5} e^{\sqrt{x}} \cdot \sin(x)\ dx$.
Именно в таких случаях определенный интеграл можно рассчитать только приближенно с какой-то точностью/погрешностью. И тогда на помощь приходит, например, метод левых прямоугольников.
💡 Кстати, наша программа универсальна! Мы можем свободно рассчитывать произвольные определенные интегралы. Для этого надо в коде программы корректно записать подынтегральную функцию.
Геометрически определенный интеграл выражает площадь криволинейной трапеции (рис. 2). Площадь — величина положительная, а значение определенного интеграла может быть отрицательным. Получается какая-то нестыковка!
💡 Используя метод левых прямоугольников, мы рассчитываем именно значение определенного интеграла!
Давайте вернемся к нашей функции $f(x) = -x^2 + 6x + 7$ и проинтегрируем ее на отрезке $[-5;\ -1] \rightarrow \int\limits_{-5}^{-1} (-x^2 + 6x + 7)\ dx$. Результат получим 2 способами: используя формулу Ньютона-Лейбница и программным путем.
Применим формулу Ньютона-Лейбница и получим:
$F(x) = -\frac{x^3}{3} + 3x^2 + 7x$
$F(-5) = \frac{125}{3} + 3 \cdot 25+ 7 \cdot (-5) = \frac{125}{3} + 40$
$F(-1) = \frac{1}{3} + 3\ -\ 7 = \frac{1}{3}\ -\ 4$
$\int\limits_{-5}^{-1} (-x^2 + 6x + 7)\ dx = F(-1)\ -\ F(-5) = \frac{1}{3}\ -\ 4\ -\ (\frac{125}{3} + 40) = -85.333333$.
Программа выдает следующий результат ($EPS = 0.0000001$, вывод до $7$-го знака после запятой):
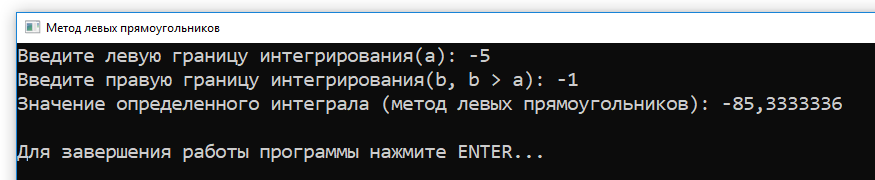
Рисунок 12 — Получение отрицательного значения определенного интеграла
➡ Чтобы достичь такой высокой точности, программе пришлось разбивать отрезок интегрирования $[-5;\ -1]$, только вдумайтесь (!), на $335\ 544\ 320$ равных шага. Да, программа выполнялась около $20$ секунд.
Чем и хорошо программирование, что всю работу можно возложить на плечи процессора, задав ему необходимую точность расчета.
А теперь посмотрим на криволинейную трапецию, которая соответствует функции $f(x) = -x^2 + 6x + 7$ на отрезке $[-5;\ -1]$ (рис. 13).
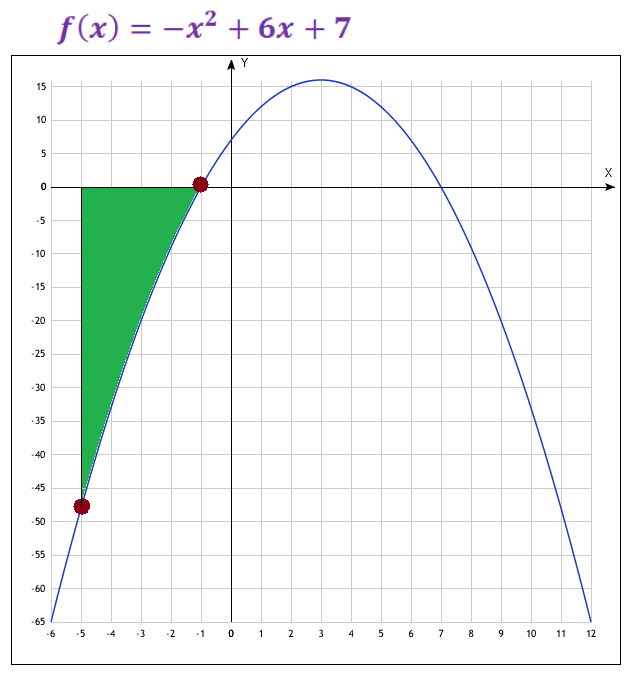
Рисунок 13 — Криволинейная трапеция, лежащая ниже оси абсцисс
Думаю, всем очевидно, что площадь зеленой фигуры — величина положительная. А чему равное значений этой «зеленой площади»? Правильно! Это значение $85.333333$.
Поэтому будьте предельно внимательны, когда требуется рассчитать значение определенного интеграла и площадь криволинейной трапеции. С одной стороны, эти значения могут совпасть до микрона, а с другой — иметь противоположный по модулю знак.
Повторю: наша цель — написать программу, которая вычисляет значение определенного интеграла с заданной точностью, а не площадь криволинейной трапеции. И пока что наш программный код хорошо с этим справляется.
Внимательный читатель, когда анализировал код программы, наверное, обратил внимание, что одним из параметров вычислительной функции является указатель на функцию. Да, это тот редкий случай, когда указатели на функцию могут очень сильно пригодиться. Разберем следующую задачу и запрограммируем ее на языке Си (стандарт С89).
Пользователю требуется выбрать $1$ из $4$ заданных функций, ввести границы интегрирования и, используя метод левых прямоугольников, получить результат с точностью $EPS = 0.001$.
На выбор пользователю предлагаю следующие функции (обратите внимание, что все они зависят только от одного аргумента $x$):
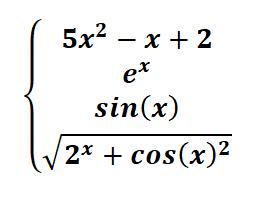
Так как метод левых прямоугольников требует, чтобы интегрируемая функция была непрерывной на заданном отрезке $[a;\ b]$, то сначала нам придется понять, какая область определения заданных $4$-рех функций.
- Посмотрим на первую функцию $f_1(x) = 5x^2 — x + 2$. Это квадратичная функция, поэтому ее область определения — любое число. Здесь нет никаких тонкостей.
- Посмотрим на вторую функцию $f_2(x) = e^x$. Это классическая экспонента, которая существует при любых значениях $x$. Здесь нет никаких тонкостей.
- Посмотрим на третью функцию $f_3(x) = sin(x)$. Еще со школьной скамьи известно, что областью определения этой функции является множество всех действительных чисел. Здесь нет никаких тонкостей.
- Посмотрим на четвертую функцию $f_4(x) = \sqrt{2^x + cos^2(x)}$. Подкоренное выражение не может принять отрицательные значения, поэтому здесь можно подставлять любые значения $x$.
В итоге в коде программы мы будем выбирать функцию и задавать границы отрезка интегрирования $[a;\ b]$. Программа, используя метод левых прямоугольников, будет нам рассчитывать значение определенного интеграла для выбранной пользователем функции с точностью $EPS = 0.001$.
➡ Количество разбиений отрезка $[a;\ b]$, то есть значение $n$ мы не будем вводить с клавиатуры, так как нам задали конкретную точность вычисления.
Обратите пристальное внимание на то, как в этой программе пригождается указатель на функцию!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 |
#include <stdio.h> #include <math.h> #include <locale.h> #include <conio.h> #include <Windows.h> // функция f1(x) = 5x^2 -x + 2 double F1(const double px) { return (5 * pow(px, 2) - px + 2); } // функция f2(x) = e^x double F2(const double px) { return (exp(px)); } // функция f3(x) = sin(x) double F3(const double px) { return (sin(px)); } // функция f4(x) = sqrt(2^x + cos(x)^2) double F4(const double px) { return (sqrt(pow(2, px) + pow(cos(px), 2.0))); } // метод левых прямоугольников (вычисление определенного интеграла) double LeftSquares(double (*pfunc)(const double), const double pa, const double pb, const unsigned int pn) { double square; // хранит приближенное значение определенного интеграла double h; // шаг табулирования (ширина прямоугольников) unsigned int i; // счетчик цикла (количество прямоугольников) // вычисляем шаг интегрировавания h = (pb - pa) / pn; square = 0.0; // просматриваем весь отрезко интегрирования for(i = 0; i < pn; i++) square += pfunc(pa + i * h); // вычисляем значение функции в заданной точке square *= h; // получаем окончательный ответ // в качестве ответа функция возвращает приближенное значение определенного интеграла return square; } // меню для выбора функции int SelectFunction(void) { int sel; printf("\nВыберите функцию для интегрирования на отрезке:"); printf("\n\t1: f(x) = 5x^2 - x + 2"); printf("\n\t2: f(x) = e^x"); printf("\n\t3: f(x) = sin(x)"); printf("\n\t4: f(x) = корень(2^x + cos^2(x)):"); printf("\n\t5: Выход из программы"); printf("\nВыбор: "); scanf("%d", &sel); return sel; } // главная функция проекта (точка входа) int main(void) { #define EPS 0.001 // точность вычислений double a, b; // границы интегрирования unsigned int n; // количество разбиений отрезка интегрирования double (*func)(const double); // указатель на функцию с одним вещественным константным аргументом double I1, I2; // значение определенного интеграла (когда n = i, n = 2i) int iselect; // номер функции, которую выбрал пользователь // настройка заголовка консольного окна программы static const TCHAR* title = TEXT("Метод левых прямоугольников"); SetConsoleTitle(title); setlocale(LC_ALL, ""); // русификация диалогов программы do { iselect = SelectFunction(); // пользователь выбирает функцию для интегрирования на отрезке switch(iselect) { case 1: { func = F1; // связываем указатель с 1ой функцией break; } case 2: { func = F2; // связываем указатель со 2ой функцией break; } case 3: { func = F3; // связываем указатель с 3ей функцией break; } case 4: { func = F4; // связываем указатель с 4ой функцией break; } } // выходим из цикла, если пользователь выбрал "Выход из программы" if(iselect == 5) break; // ввод с клавиатуры границ интегрирования printf("\nВведите левую границу интегрирования(a): "); scanf("%lf", &a); printf("Введите правую границу интегрирования(b, b > a): "); scanf("%lf", &b); n = 2; // стартовое количество разбиений отрезка интегрирования // считаем значение определенного интеграла для n1 = 10 I1 = LeftSquares(func, a, b, n); n *= 2; // увеличиваем вдвое количество разбиений // считаем значение определенного интеграла для n2 = 20 (2n1) I2 = LeftSquares(func, a, b, n); // используем правило Рунге для достижения заданной точности (EPS = 0.0001) while(1.0/3.0 * fabs(I2 - I1) >= EPS) { I1 = I2; n *= 2; // на каждой итерации количество разбиений увеличивается вдвое I2 = LeftSquares(func, a, b, n); } // выводим приближенное значение определенного интеграла с точностью до 5 знаков printf("Значение определенного интеграла (метод левых прямоугольников): %0.5lf", I2); getch(); // задержка работы программы, чтобы была возможность просмотреть результат } while(1); return 0; // передача управления в ОС (официальное закрытие работы программы) } |
А вот результаты работы программы для каждой из $4$-рех заданных функций:
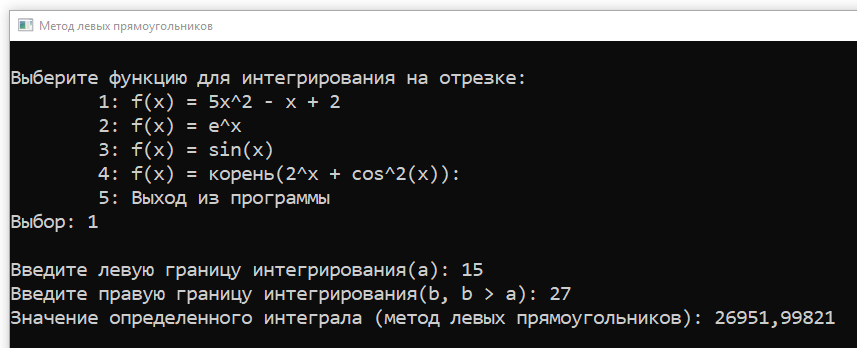
Тест 1 — Работа с функцией №1
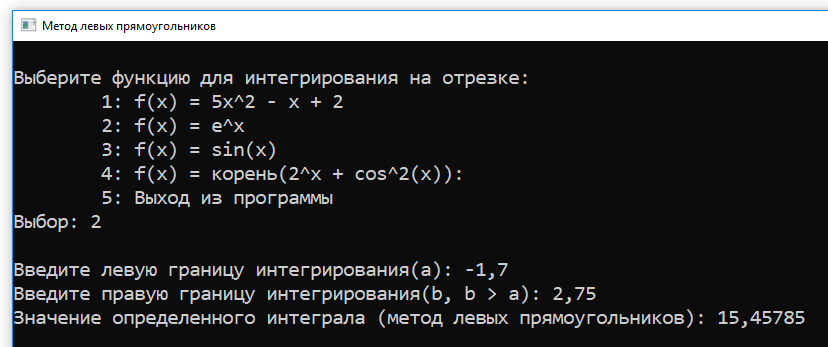
Тест 2 — Работа с функцией №2
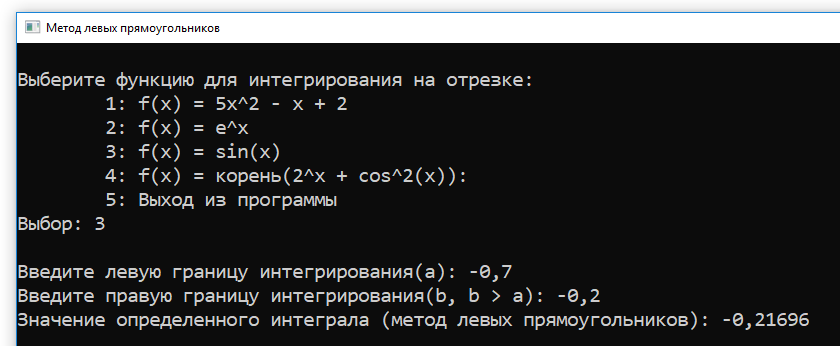
Тест 3 — Работа с функцией №3
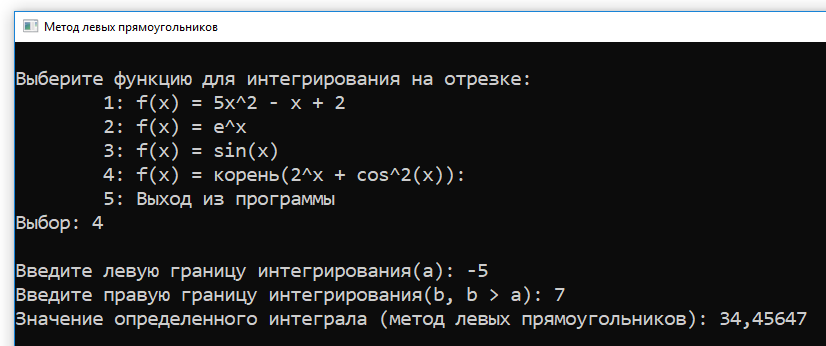
Тест 4 — Работа с функцией №4
➡ При этом вы должны понимать, что программа масштабируема!
Можно добавить в меню еще любое количество нужных функций и интегрировать их на заданном отрезке $[a;\ b]$, используя приближенный численный расчет, называемый метод левых прямоугольников.
Хочу также заметить такой момент — если указать широкий отрезок интегрирования $[a;\ b]$ и высокую точность расчетов ($EPS$), то программные вычисления могут выполняться дольше минуты.
Давайте проверим, сколько времени потребуется программе, чтобы найти приближенное значение $4$-ой функции при таких параметрах $\rightarrow$ $\int\limits_{-30}^{+25} (\sqrt{2^x + \cos^2(x)})\ dx$, а также узнаем, на какое количество равных шагов потребовалось разбить отрезок интегрирования $[-30;\ 25]$, чтобы добиться заданной точности $EPS = 0.001$.
➡ В итоге программа выполнялась $27.745$ секунд, а значение $n$ составило $67\ 108\ 864$. Если увеличить точность до одной миллионой и расширить отрезок интегрирования $[a;\ b]$ до сотен, то программа вообще может «вычисляться» дольше суток 🙂 .
На узких отрезках $[a;\ b]$ программа, как правило, отрабатывает за несколько сотых секунды.
В итоге мы детально рассмотрели метод численного интегрирования, называемый методом левых прямоугольников, а также закодировали этот метод на языке программирования «чистый» Си (стандарт С89).
Если у вас остались вопросы в рамках метода левых прямоугольников, что-то непонятно в программном коде рассмотренного метода, то оставляйте свои комментарии под этой статьей или пишите мне на электронный адрес proglabs@mail.ru.
Добавить комментарий