В данном материале я хочу показать несколько вариантов бинарного дерева поиска. Мы не будем здесь обсуждать алгоритмы построения этих деревьев и пр. Давайте просто посмотрим, какими они бывают, и это лишь малая-малая часть того, с чем можно столкнуться на практике.
Классическое двоичное дерево поиска, состоящее из нескольких вершин, имеет примерно такой вид.
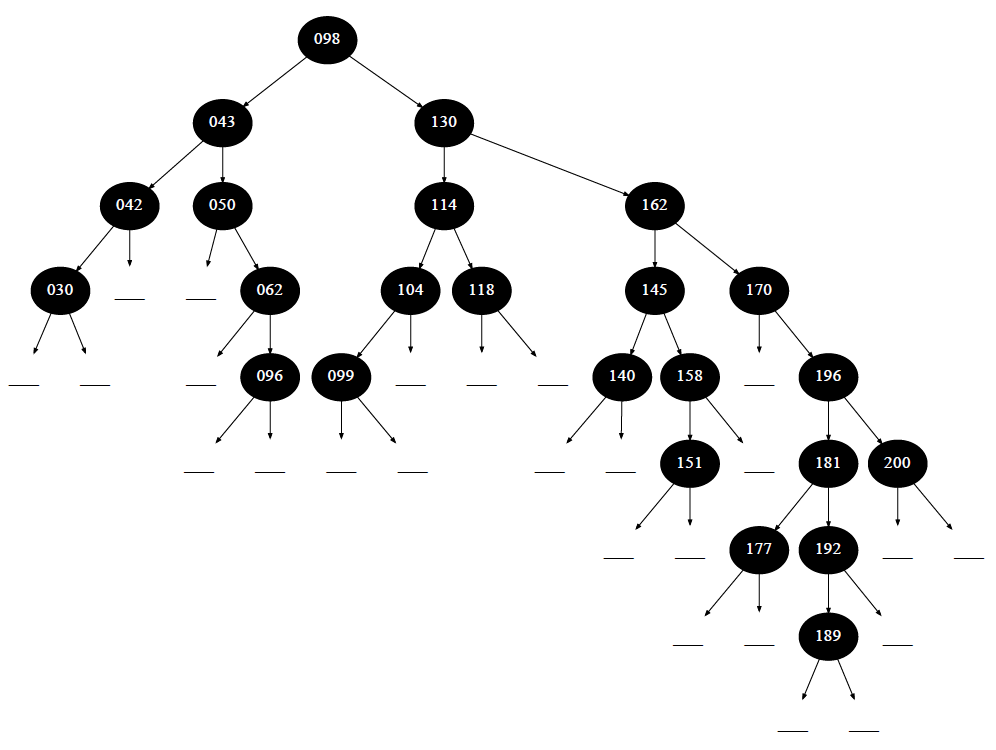
Широкое дерево, состоящее из большого количество узлов.
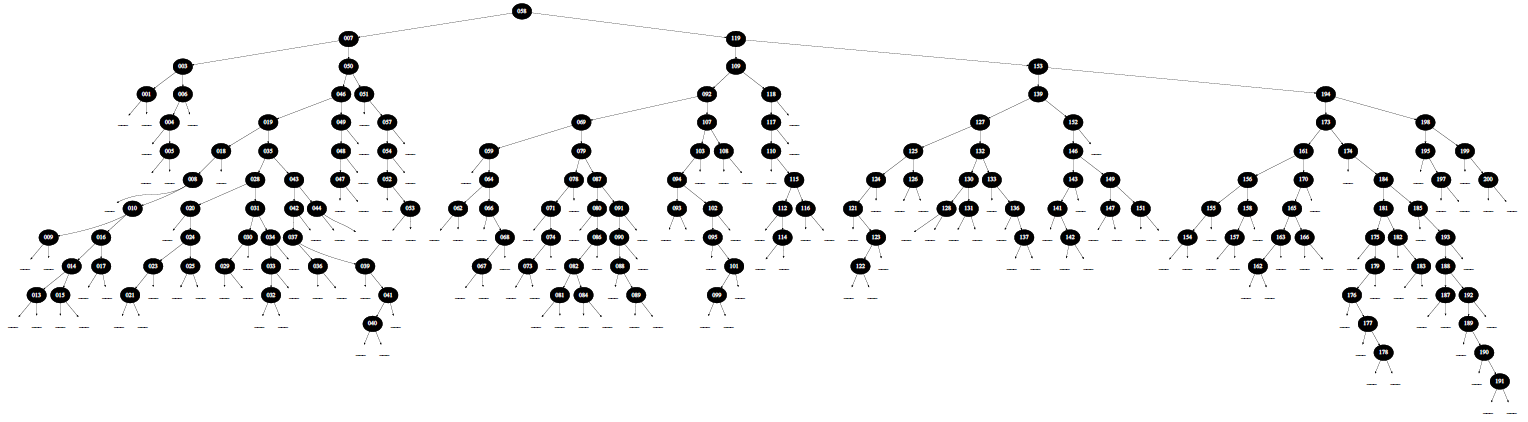
А это дерево выродилось в простой линейный список, утратив все свои полезные свойства.
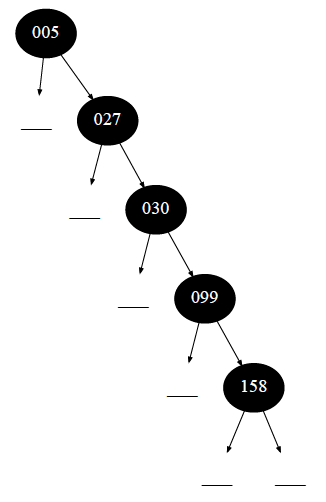
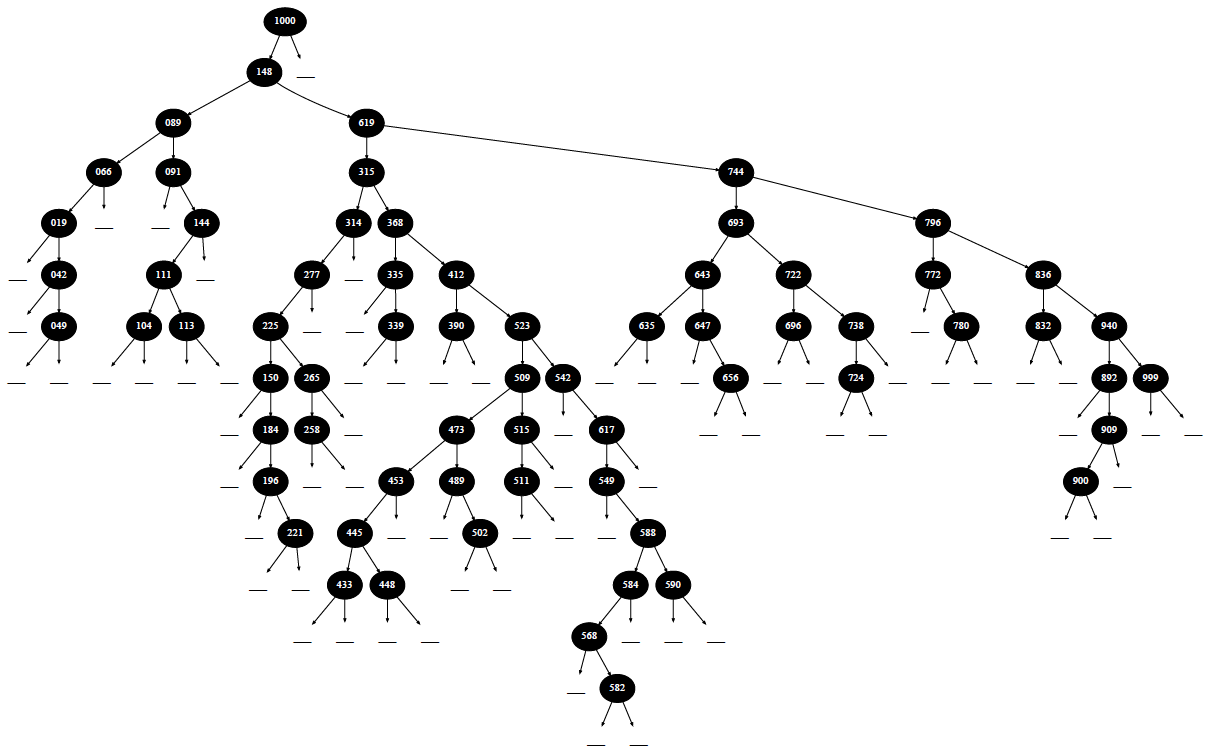
Это пример сильноветвящегося двоичного дерева поиска, состоящего из нескольких сотен вершин.
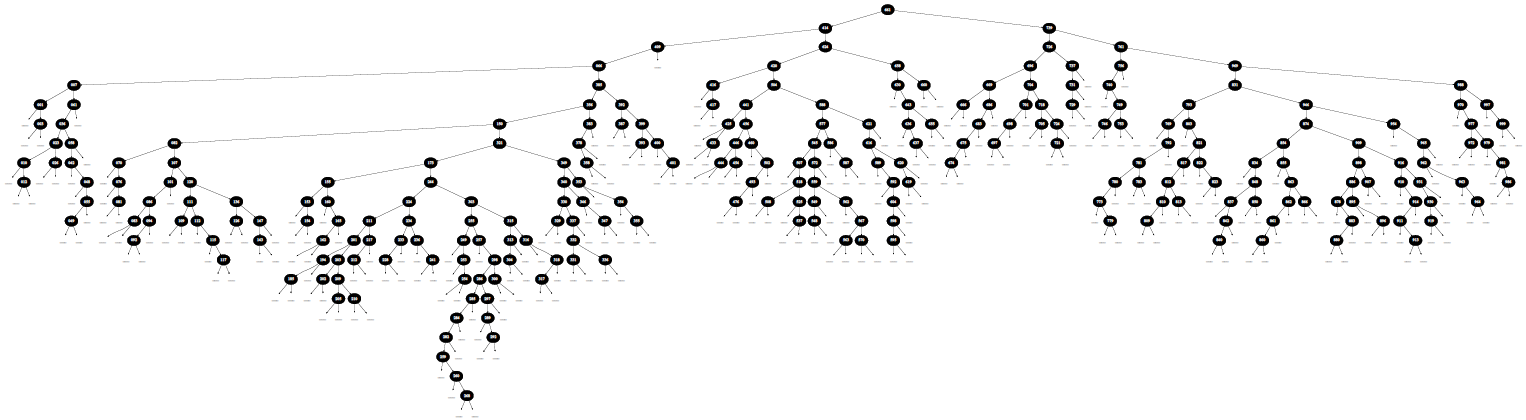
А это дерево перекосило в левую сторону. И такое бывает, когда значение ключа первого добавленного узла в дерево является максимальным среди всех ключевых значений.
А это сбалансированное дерево поиска. Такие деревья называют AVL-деревьями. Эти деревья обладают замечательными поисковыми характеристиками, но достаточно сложны в обслуживании, так как при добавлении / удалении вершин необходимо иногда проводить балансировку дерева.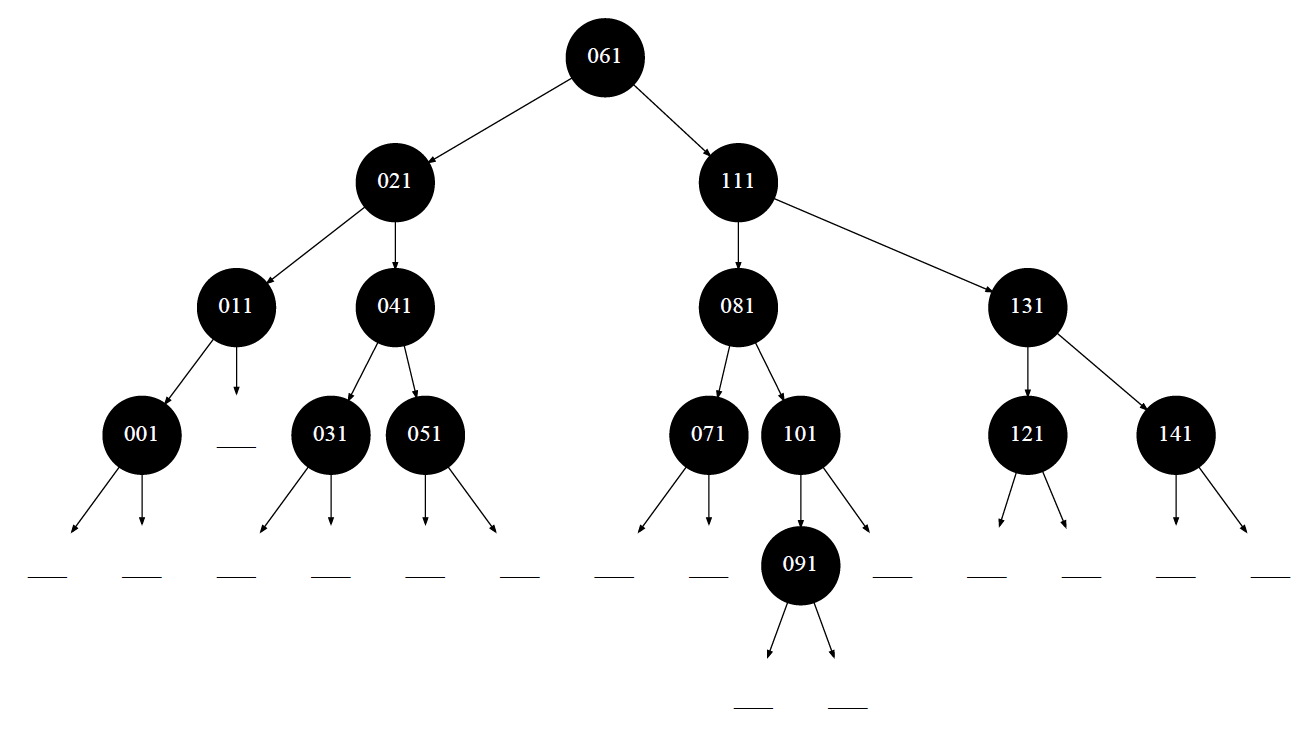
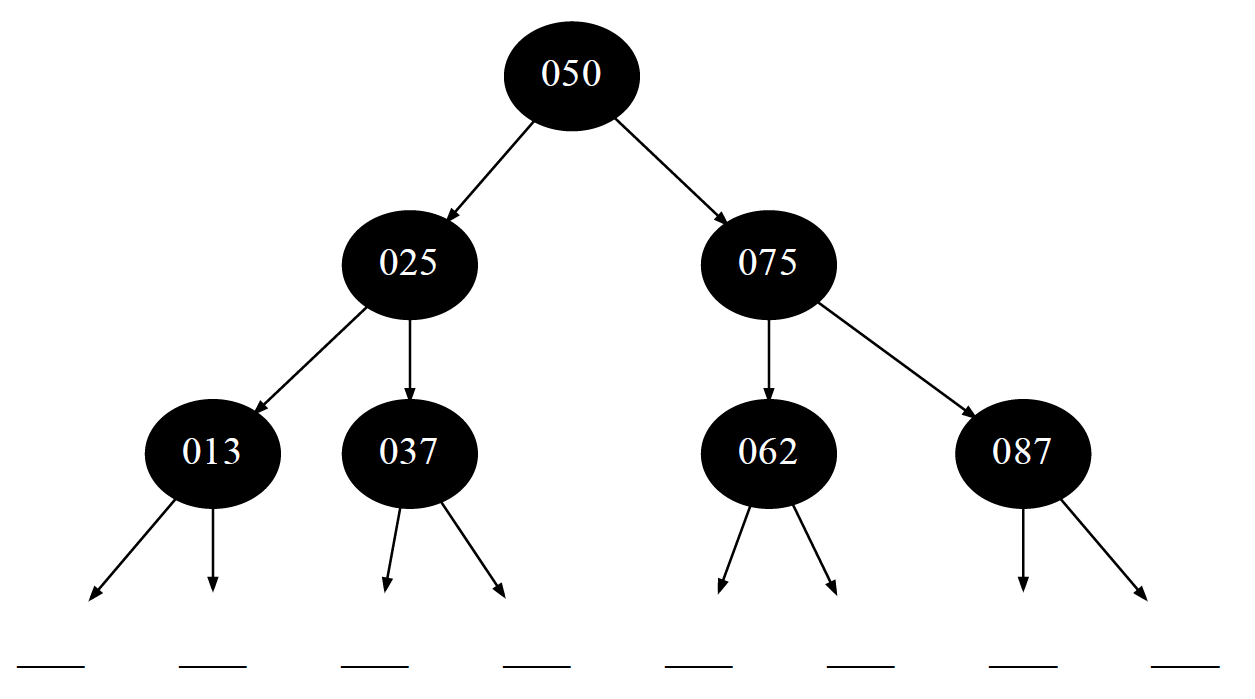
А это редчайший тип двоичного дерева поиска — идеально сбалансированное дерево поиска ( ИСДП ). Обратите внимание, что последний уровень ( листовой уровень ) полностью заполнен. На практике такое поисковое дерево получить практически невозможно.
А в этом дереве ключом узлов выступают не целые числа, а строковые значения, но при этом оно является двоичным деревом поиска.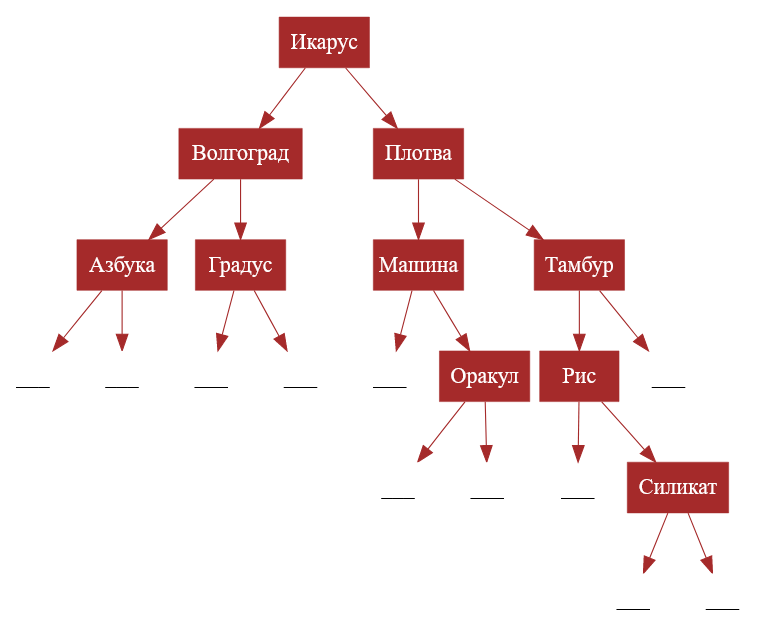
А у этого поискового двоичного дерева ключом узлов выступают символьные значения.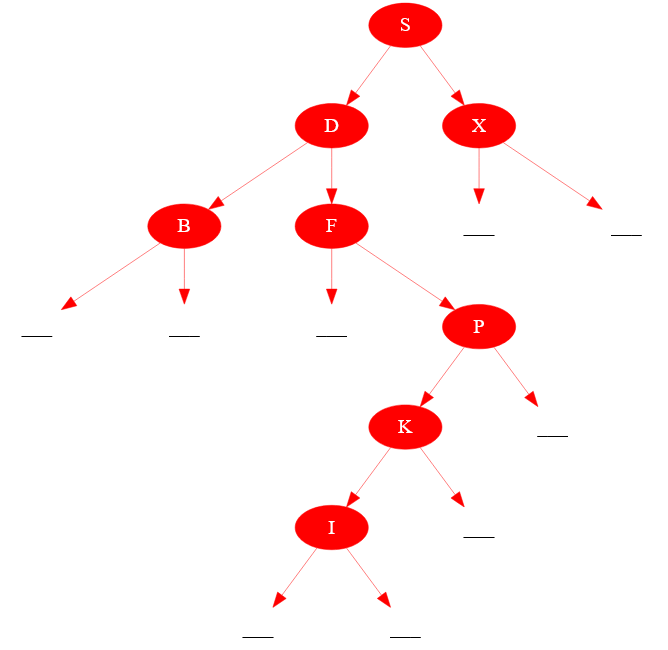
Иногда, если заранее обговорить этот момент, можно физически добавлять в дерево узлы с дублирующими ключами. Дублирующие элементы поискового дерева выделены синим цветом. Но на практике так поступают крайне редко, так как есть другие, более эффективные способы решения такой проблемы.
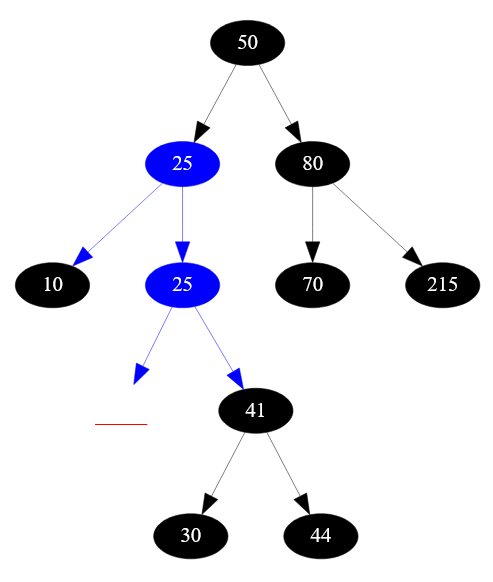
Чтобы при вставке нового узла в дерево учитывать дублирующие элементы достаточно завести счетчик дубликатных значений. В этом случае нет никакой необходимости физической вставки дублирующей вершины в поисковое двоичное дерево. Топология дерева в этом случае примет примерно такой вид:
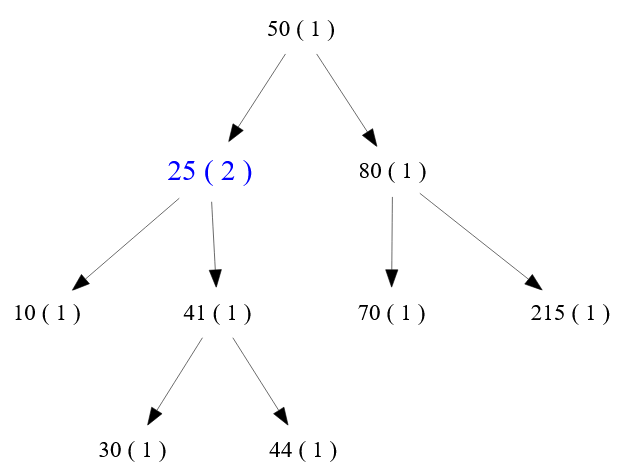
💡 В дальнейшем анализе будем использовать дерево примерно такой топологии. Это среднее по характеристикам двоичное дерево поиска: нет сильных перекосов, нет балансировки.
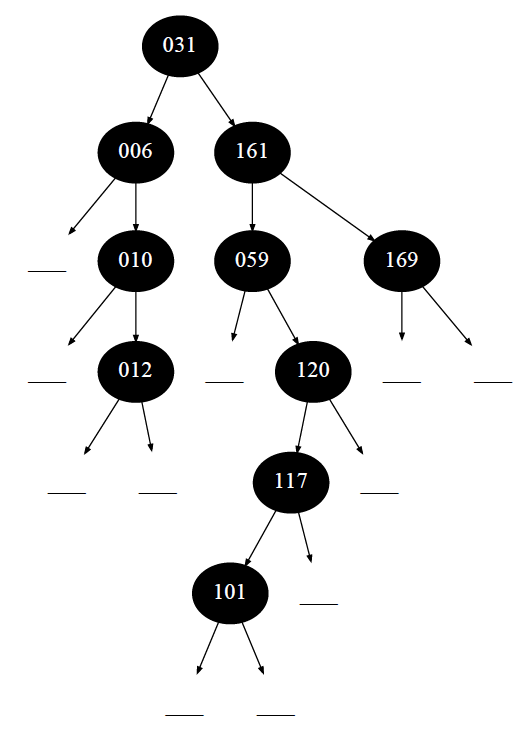
Обращаю ваше внимание, что на данной странице я лишь показываю графическое представление бинарных поисковых деревьев. Все операции над этой древовидной структурой будут рассмотрены в следующих главах.
➡ Просмотреть двоичное дерево поиска, состоящее примерно из 200-250 узлов ( pdf-файл ).
➡ Пишите в комментариях, какие виды двоичных деревьев хотели бы еще дополнительно увидеть.
Добавить комментарий