Обход бинарного дерева

ВНИМАНИЕ

Для заказа программы на бинарное дерево поиска пишите на мой электронный адрес proglabs@mail.ru

Посмотрим на следующее двоичное поисковое дерево. Ничем не примечательное. Обыкновенное, среднестатистическое бинарное дерево, состоящее из $11$ вершин.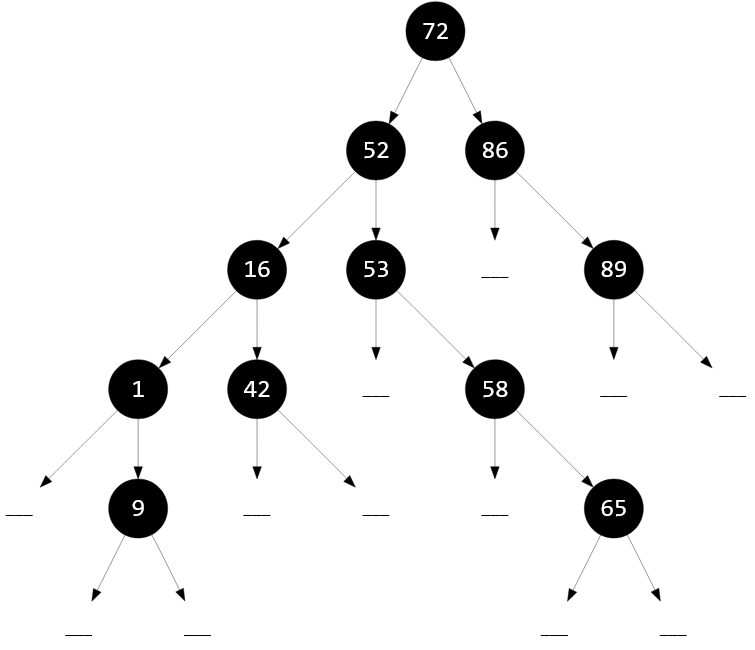

Хорошо, когда под рукой есть различные визуализаторы деревьев, но обычно на практике студенты пишут консольные программы, например, в среде разработки Visual Studio на языках C/C++.

Чтобы распечатать ключевые значения, а также данные узлов, требуется каким-то образом «просканировать» дерево, выводя нужную информацию на консоль ( реже в файл ). Для этих целей и используют обходы.

💡 Основная цель обхода — посетить каждую вершину поискового дерева ровно $1$ раз. Этого достаточно, чтобы «достать» из вершины любую информацию.

Фундаментально дерево можно «сканировать» $3$ различными способами:

• сверху вниз;
• снизу вверх;
• симметрично относительно вершины;

Но, так как каждый узел дерева имеет левое и правое поддерево, то каждый из этих $3$ способов еще раздваивается, и в итоге образуется всего $6$ различных вариантов обхода бинарного дерева поиска.

В теории программирования эти обходы имеют официальные названия:

• прямой левый;
• прямой правый;
• обратный левый;
• обратный правый;
• симметричный левый;
• симметричный правый.

Лично я предпочитаю такую нотацию:

Левый	Корень	Правый
L	K	P

Сведу информацию о названиях обходов дерева в следующую таблицу:

#	Официальное название	Мое название
1	Прямой левый	KLP
2	Прямой правый	KPL
3	Обратный левый	LPK
4	Обратный правый	PLK
5	Симметричный левый	LKP
6	Симметричный правый	PKL

➡ Обход под #5 я неспроста выделил красным цветом — это самый популярный обход двоичного поискового дерева. Почему? Ниже об этом расскажу.

В целом любой из $6$ обходов достаточно легко программируется рекурсивно ( хотя существуют и итеративные реализации ). Рассмотрим детальнее общий концепт обходов на примере симметричного левого обхода ( или LKP ).

Как следует из названия, сначала нужно что-то делать «слева», затем с корнем, и в завершении «справа». Идея такая: пока можно идти влево по дереву — спускаемся влево; достигли NULL — поднимаемся вверх и распечатываем ключ ( и при необходимости данные ) текущего узла; после этого сворачиваем направо и идем до 1-ой развилки и опять при первой возможности сворачиваем налево, где идем до упора.

То есть в процессе симметричного левого обхода постоянно «магнитом» тянет влево. Как только есть возможность свернуть налево — сворачиваем и идем по левым связям до упора ( до NULL ).

Визуальный пример симметричного левого обхода бинарного дерева поиска имеет такую топологию: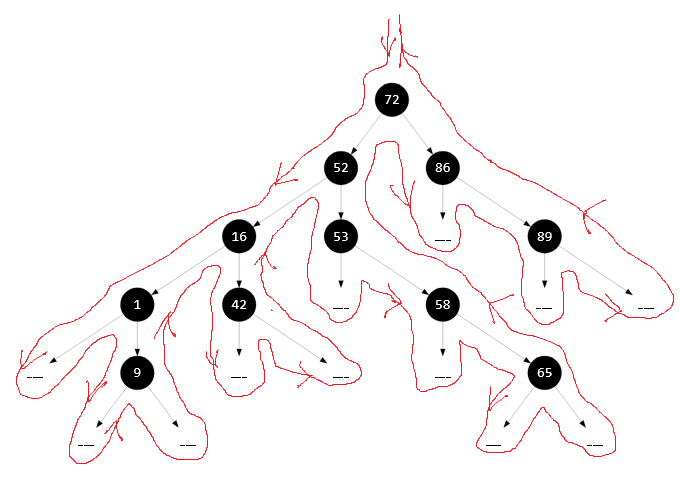

В результате LKP-обхода на экран будут распечатаны ключи в таком порядке:
$\qquad1$, $9$, $16$, $42$, $52$, $53$, $58$, $65$, $72$, $86$, $89$.
Как видно из этой последовательности чисел — она является возрастающей последовательностью ( или отсортированной по возрастанию ).

➡ Именно по этой причине такой обход поискового двоичного дерева имеет бешеную популярность в различных программах.

Рекурсивная программная функция LKP-обхода имеет следующий вид:

Обращаю ваше внимание, что это тот редкий случай, когда функция, работающая с бинарным деревом, возвращает в качестве результата void, а не какое-то конкретное значение ( обычно указатель на корень или конкретный узел дерева ).

Для этого дерева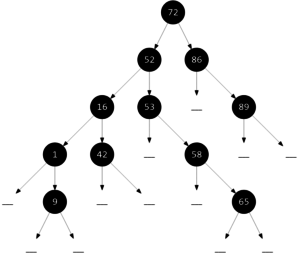

были получены следующие результаты при различных его обходах:

#	Тип обхода	Расшифровка обхода	Последовательность ключей
1	KLP	корень — левый — правый	$72,\ 56,\ 16,\ 1,\ 9,\ 42,\ 53,\ 58,\ 65,\ 86,\ 89$
2	KPL	корень — правый — левый	$72,\ 86,\ 89,\ 52,\ 53,\ 58,\ 65,\ 16,\ 42,\ 1,\ 9$
3	LPK	левый — правый — корень	$9,\ 1,\ 42,\ 16,\ 65,\ 58,\ 53,\ 52,\ 89,\ 86,\ 72$
4	PLK	правый — левый — корень	$89,\ 86,\ 65,\ 58,\ 53,\ 42,\ 9, 1,\ 16,\ 52,\ 72$
5	LKP	левый — корень — правый	$1,\ 9,\ 16,\ 42,\ 52,\ 53,\ 58,\ 65,\ 72,\ 86,\ 89$
6	PKL	правый — корень — левый	$89,\ 86,\ 72,\ 65,\ 58,\ 53,\ 52,\ 42,\ 16,\ 9,\ 1$

💡 Очевидно, что наибольший интерес представляют именно симметричные обходы ( LKP, PKL ), так как в этом случае ключи вершин поискового дерева образуют упорядоченную последовательность.

Возникает закономерный вопрос: а зачем нужны остальные типы обходов, кроме симметричных? Дело в том, что каждый из этих $6$ типов обходов имеет практическое значение! Например, при рекурсивном удалении всего двоичного дерева из памяти нужно последовательно удалять все его вершины, начиная с самых «нижних» ( листовых ). И в этом сильно поможет один из обратных обходов( LPK, PLK ).

Также я хочу привести программную реализацию всех $6$ обходов бинарного дерева поиска.

Но это еще не все! Иногда нужно вывести значения вершин по уровням поискового дерева: сначала все вершины $0$-го уровня ( на этом уровне находится только одна вершина — корень дерева ); затем все вершины $1$-го уровня ( на этом уровне находятся дети корневой вершины ); затем все вершины $2$-го уровня ( на этом уровне лежат дети вершин $1$-го уровня ) и так далее.

Нумерация уровней мной взята условно. Иногда дерево нумеруют, начиная с уровня #1. Здесь нет четки правил, но это и не столь важно.

Поуровневый вывод данных вершин для этого дерева

показан в следующей таблице:

# уровня	Значения ключей вершин
0	$72$
1	$52,\ 86$
2	$16,\ 53,\ 89$
3	$1,\ 42,\ 58$
4	$9,\ 65$

О том, как реализовать поуровневый вывод двоичного дерева поиска я расскажу в одной из следующих заметок, а пока пишите в комментариях, какие выводы поисковых деревьев вам еще известны.

➡ Кстати, стоит сказать, что обход нужен при сортировке двоичным деревом. Это такая специальная сортировка данных, для упорядочивания которых строится бинарное дерево поиска. После построения дерева запускается симметричный обход ( левый или правый — зависит от того, по возрастанию или убыванию данные нужно отсортировать ) и данные из узлов дерева переписываются обратно в исходный массив.

ВНИМАНИЕ

Для заказа программы на бинарное дерево поиска пишите на мой электронный адрес proglabs@mail.ru