| ВНИМАНИЕ | Для заказа программы на двоичное поисковое дерево пишите на мой электронный адрес proglabs@mail.ru |
Операция удаления вершины из двоичного дерева по сравнению с операциями вставки, поиска и обхода наиболее сложная. Правда есть еще такая сложная операция, как балансировка дерева, но она не является стандартной для двоичного дерева поиска. Балансировку проводят в AVL-деревьях.
Хочу показать анонимное поисковое дерево ( без привязки к ключам ), состоящее из $10$ вершин.
💡 При удалении очень важно следить за статусом удаляемой вершины. Любая вершина в любом бинарном дереве имеет один из трех статусов:
| # | Статус | Количество детей | Примечание |
| 1 | Пустая ( лист ) | $0$ | Левый и правый указатель указывают в NULL |
| 2 | Половинчатая | $1$ | Левый или правый указатель указывает в NULL, но не оба одновременно |
| 3 | Полная | $2$ | Левый и правый указатель не указывают в NULL |
Посмотрим на листовые узлы анонимного поискового двоичного дерева ( они выделены красным цветом ):

Рисунок — листовые узлы бинарного дерева поиска
Также рассмотрим половинчатые узлы дерева ( они выделены синим цветом ):
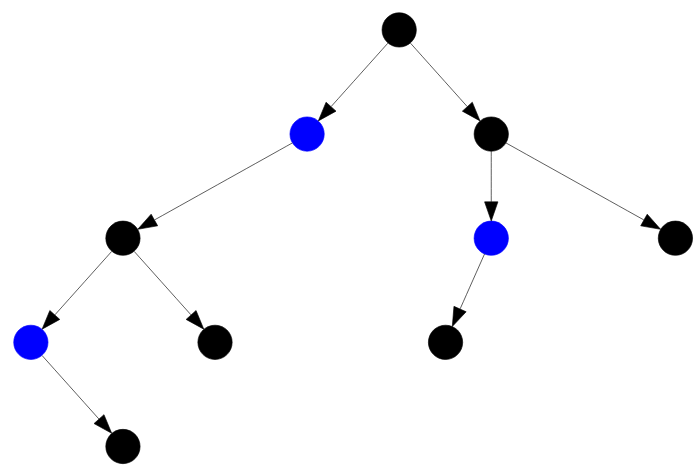
Рисунок — половинчатые узлы бинарного дерева поиска
И осталось рассмотреть полные узлы дерева ( они выделены цветом морской волны ). Каждый полный узел имеет двух сыновей.
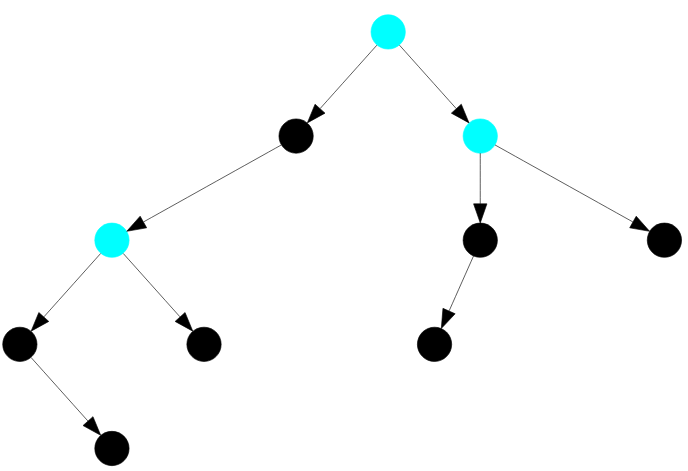
Рисунок — полные узлы бинарного дерева поиска
А сейчас я хочу посмотреть статусы всех узлов на одном двоичном дереве поиска ( напомню: красные — листья; синие — неполные; морской волны — полные узлы ):
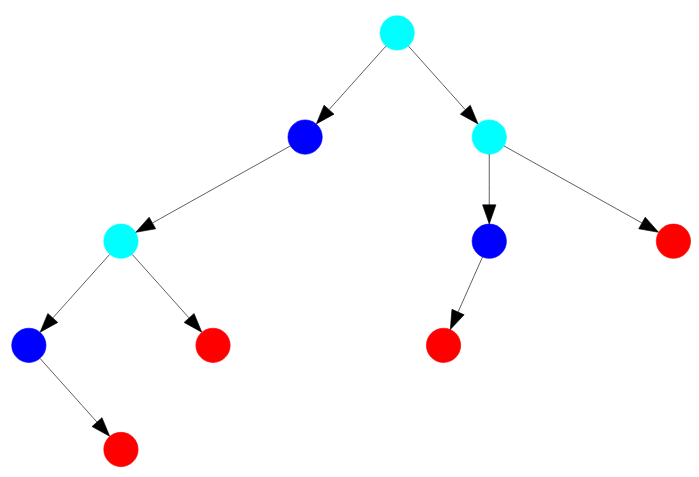
Рисунок — статусы узлов бинарного дерева поиска
Очевидно, что нужна специальная программная функция, которая определяет статус заданного узла двоичного дерева поиска. У меня получилась следующая функция:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//------------------------------------------------------------------------------ // определение статуса заданного узла ( лист, половинчатый или полный ) // root - указатель на проверяемый узел ( не должен быть нулевым ) // в качестве ответа возвращается статус проверяемого узла дерева //------------------------------------------------------------------------------ Node_status Get_status_node( const Node* const root ) { // по умолчанию принимаем, что проверяемый узел является половинчатым Node_status status = HALF; // проверка на лист ( нет ни одного сына ) if ( ( root -> left == NULL ) and ( root -> right == NULL ) ) { status = EMPTY; } else { // проверка на полный узел ( имеет обоих сыновей ) if ( ( root -> left != NULL ) and ( root -> right != NULL ) ) { status = FULL; } } return status; } //------------------------------------------------------------------------------ |
Дополнительно мне пришлось описать перечисление следующего вида:
|
1 2 3 4 5 6 7 8 9 10 |
//------------------------------------------------------------------------------ // статус узла бинарного дерева поиска //------------------------------------------------------------------------------ typedef enum Node_status { EMPTY, // пустой узел ( лист - не имеет сыновей ) HALF, // половинчатый ( имеет одного сына: левого или правого ) FULL // полный ( имеет обоих сыновей ) } Node_status; //------------------------------------------------------------------------------ |
Показывать удаление вершин буду на этом двоичном дереве поиска:
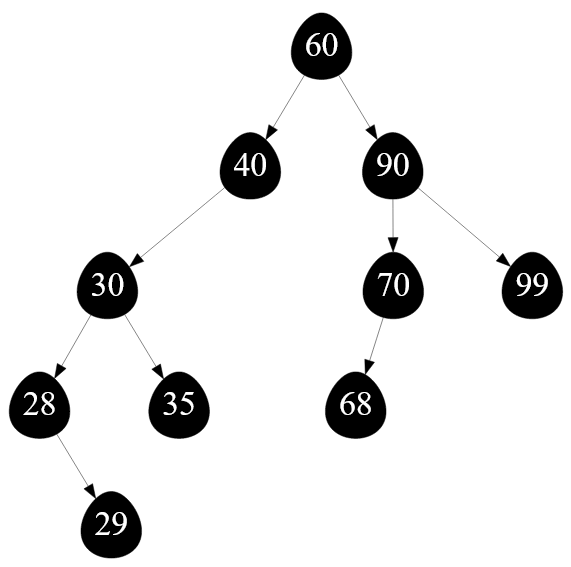
Рисунок — бинарное дерево для демонстрации операции удаления
Например, требуется удалить вершину с ключом $35$.
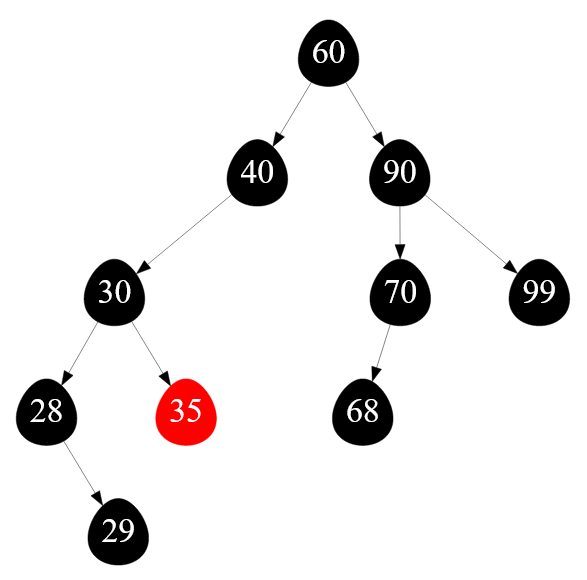
Рисунок — удаление вершины с ключом $35$
В первую очередь надо определить статус удаляемой вершины. Напомню, что вершина может быть пустой ( листовой ), половинчатой или полной. Очевидно, что удаляемая вершина является листовой, так как она не имеет сыновей.
💡 Удаление листовой вершины в двоичном дереве реализуется наиболее просто и понятно!
Для этого я удаляю эту вершину из дерева ( командой free, если речь про язык программирования «чистый» Си ) и в качестве ответа возвращаю NULL-указатель. В результате удаления узла с ключом $35$ бинарное дерево поиска примет вид:
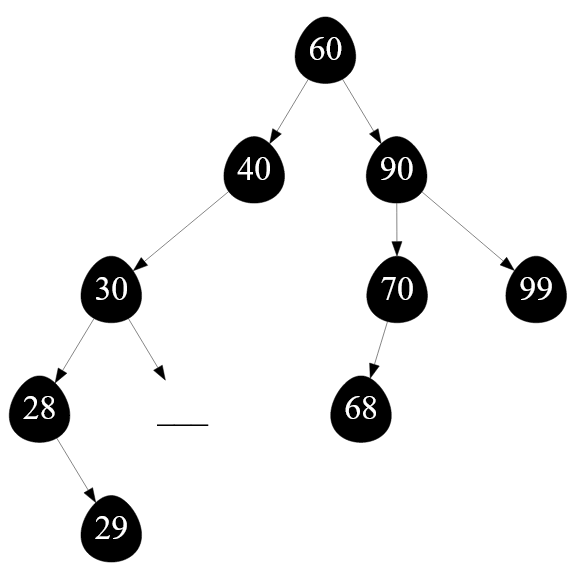
Рисунок — вид двоичного дерева после удаления вершины с ключом $35$
Сейчас я хочу удалить вершину с ключом $40$ из следующего двоичного поискового дерева:
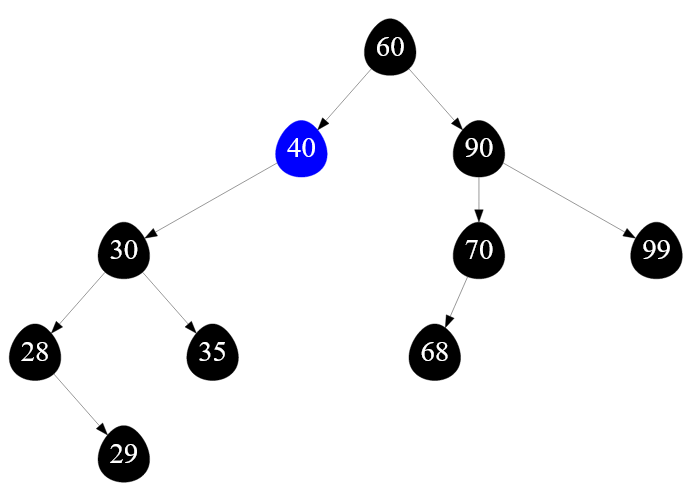
Рисунок — удаление вершины с ключом $40$
Удаляемая вершина является половинчатой, так как она имеет только одного сына ( левого ) с ключом $30$. Удалять неполные вершины из дерева чуть сложнее, чем листовые, но в целом также несложно.
Алгоритм удаления неполных узлов такой:
| ➡ | рекурсивно «спуститься» и найти удаляемый узел в бинарном дереве поиска; |
| ➡ | определить статус удаляемого узла ( очевидно, что удаляемая вершина должна иметь статус «половинчатой» ); |
| ➡ | удалить память из-под найденной вершины ( например, командой free, если реализация проходит на языке Си ); |
| ➡ | в качестве результата вернуть указатель на левое поддерево ( если удаляемый узел имел левого сына ), иначе указатель на правое поддерево. |
В моем примере удаляемая вершина с ключом $40$ имеет левого сына, значит, в качестве результата функция должна вернуть указатель на левое поддерево. У этого левого поддерева корнем выступает узел с ключом $30$.
В результате удаления элемента с ключом $40$ двоичное дерево поиска примет вид:
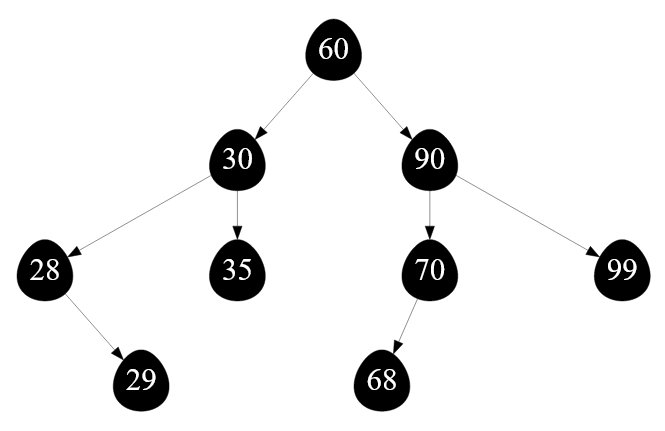
Рисунок — вид двоичного дерева после удаления вершины с ключом $40$
А сейчас хочу посмотреть на самый тяжелый вариант удаления элемента из двоичного поискового дерева. Например, надо удалить узел с ключом $60$:
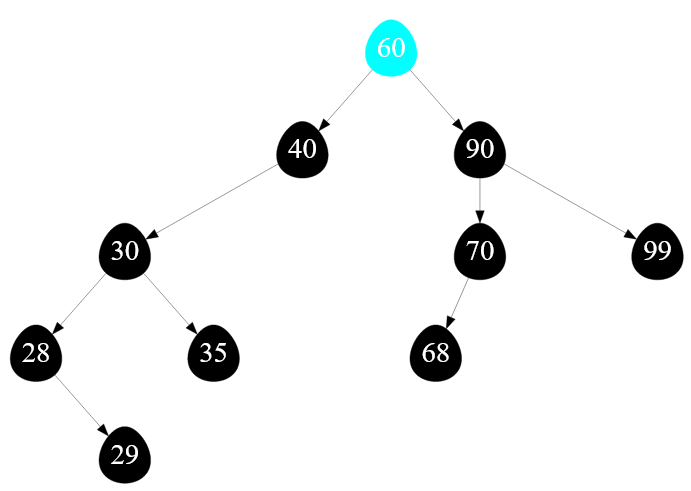
Рисунок — удаление вершины с ключом $60$
💡 Мало того, что удаляемый узел является корнем заданного дерева, так при этом он является и полным узлом, то есть имеет и левого, и правого сына.
Очевидно, что просто взять и удалить этот узел нельзя, так как после этого оба сына не будут иметь родителя. Дерево будет «порвано» и перестанет быть бинарным деревом поиска, а превратится в какую-то другую динамическую структуру данных.
Поэтому на практике поступают следующим образом:
| ➡ | рекурсивно «спуститься» и найти удаляемый узел в бинарном дереве поиска; |
| ➡ | определить статус удаляемого узла ( очевидно, что удаляемая вершина должна иметь статус «полной» ); |
| ➡ | в левом поддереве найти вершину с максимальным ключом или в правом поддереве найти вершину с минимальным ключом; |
| ➡ | договоримся, что на предыдущем этапе нашли в правом поддереве вершину с минимальным ключом и сейчас записываем это минимальное значение на место ключа удаляемой полной вершины; |
| ➡ |
удаляем из правого поддерева вершину с минимальным ключом. |
Звучит данный алгоритм непросто, да и реализуется также непросто!
Итак, моя цель удалить полный узел с ключом $60$, который по совместительству также является и корнем рассматриваемого дерева. Следуя алгоритму, нужно найти в правом поддереве вершину с минимальным значением ключа. Получаю следующую картинку:
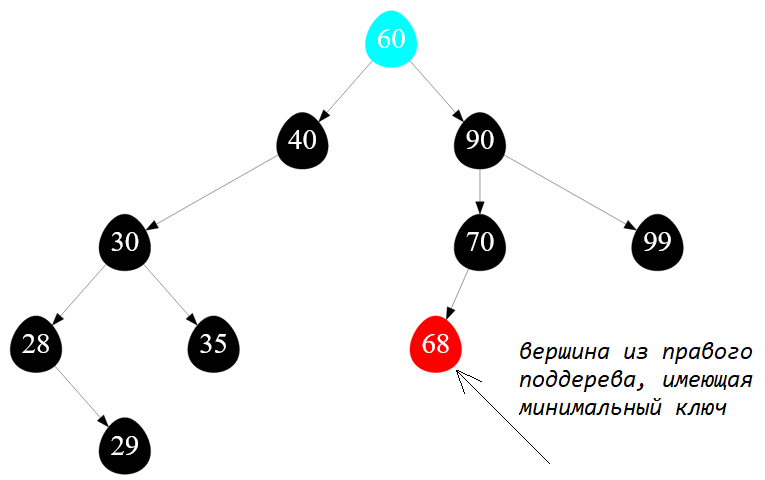
Рисунок — поиск узла с минимальным ключом в правом поддереве
Далее я следую алгоритму и записываю значение минимального ключа, то есть число $68$ вместо ключа удаляемой полной вершины, то есть вместо числа $60$. Получаю такое промежуточное состояние бинарного дерева поиска:
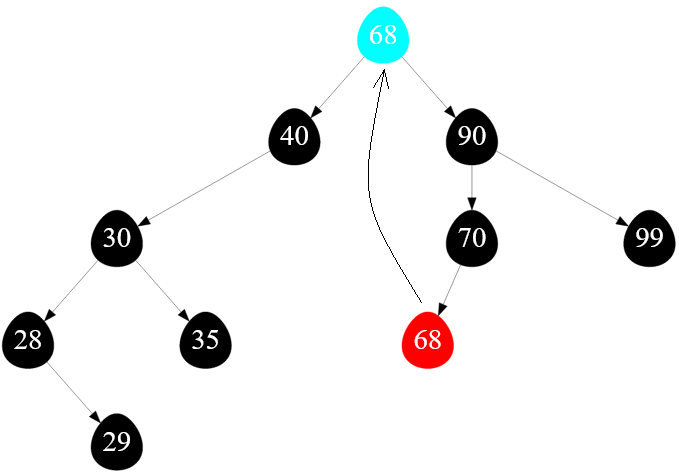
Рисунок — копируем ключ минимального элемента в полный удаляемый узел
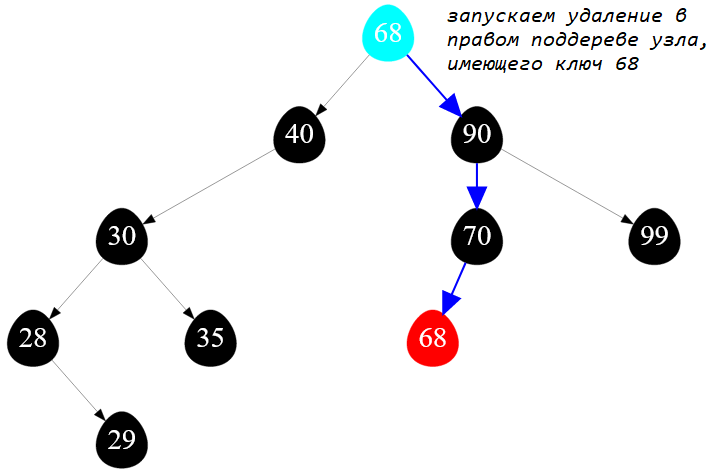
Продолжаю следовать алгоритму и запускаю удаление вершины с минимальным ключом из правого поддерева. Обращаю внимание, что вершина с минимальным значением ключа может иметь статус:
- листовая ( не имеет детей );
- неполной ( имеет правого сына ).
Никаких других статусов вершина с минимальным ключом иметь не может. Если бы она имела левого сына, это бы означало, что она сама не является минимальной.
В результате удаления узла с ключом $60$ бинарное дерево поиска примет вид:
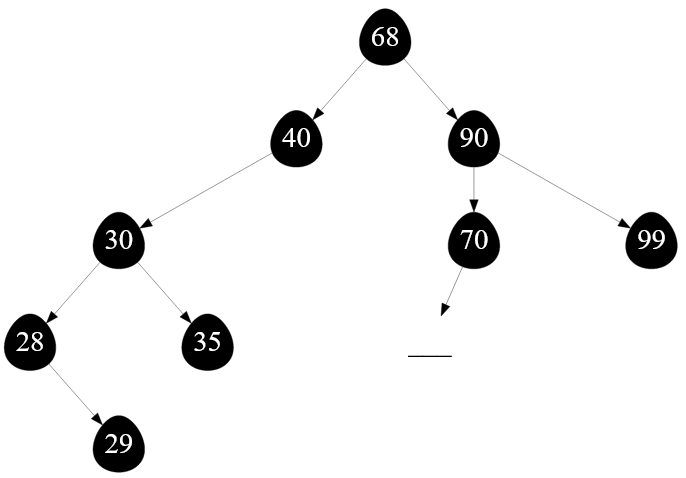
Рисунок — вид двоичного дерева после удаления вершины с ключом $60$
💡 Сразу хочу предупредить о таком моменте: правильно запрограммировать функцию, например на языке Си, гораздо сложнее, чем разобраться с алгоритмом удаления на картинках.
А это моя программная реализация на языке «чистый» Си рекурсивной функции удаления элемента из бинарного дерева поиска:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
//------------------------------------------------------------------------------ // удаление вершины из дерева, заданной ключом // если вершины с заданным ключом нет, то с деревом ничего не происходит // в качестве результата возвращается указатель на корень "обновленного" дерева //------------------------------------------------------------------------------ Node* Remove_node( Node* const root, const int key ) { if ( root == NULL ) { return NULL; } if ( key < root -> key ) { root -> left = Remove_node( root -> left, key ); } else { if ( key > root -> key ) { root -> right = Remove_node( root -> right, key ); } else // key == root -> key ( вершина с заданным ключом найдена! ) { Node_status remove_node_status = Get_status_node( root ); Node* left = root -> left; Node* right = root -> right; if ( remove_node_status == EMPTY ) { free( root ); return NULL; } if ( remove_node_status == HALF ) { free( root ); return ( left == NULL ? right : left ); } if ( remove_node_status == FULL ) { Node* min_node = Find_min_node( right ); root -> key = min_node -> key; root -> right = Remove_node( root -> right, min_node -> key ); return root; } } } return root; } //------------------------------------------------------------------------------ |
Из функции Remove_node вызывается вспомогательная функция Find_min_node. Ее реализацию я оставляю для вашей работы 🙂
Пишите в комментариях, насколько вы поняли алгоритм удаления вершины из двоичного дерева поиска.
| ВНИМАНИЕ | Для заказа программы на двоичное дерево поиска пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий