При удалении узла из двоичного дерева поиска, а также, например, при подсчете количества листьев, неполных или полных узлов дерева требуется понимать, какого типа вершина ( с точки зрения количества ее потомков ) обрабатывается. Поэтому я решил написать эту заметку-шпаргалку, в которой покажу, как можно написать крайне полезную функцию, определяющую статус вершины двоичного дерева ( поиска ).
Мне потребуется стандартное бинарное дерево ( необязательно поисковое ) для анализа. При этом мне абсолютно не важно, чему равны ключи вершин этого дерева. Поэтому буду рассматривать анонимное двоичное дерево, например, такое:

Рисунок — стандартное анонимное бинарное дерево ( поиска )
Представленное двоичное дерево состоит из $10$ вершин. Каждая вершина имеет статус, который зависит от количества ее потомков.
Узел, не имеющий сыновей, называется листом ( листовой вершиной ).
На следующем рисунке я обозначу красным цветом все листовые узлы бинарного дерева:

Рисунок — листовые вершины закрашены красным цветом
Вершина, имеющая либо левого, либо правого сына, но не обоих одновременно, называется неполной ( половинчатой ).
На следующем рисунке я обозначу синим цветом все неполные узлы двоичного дерева:
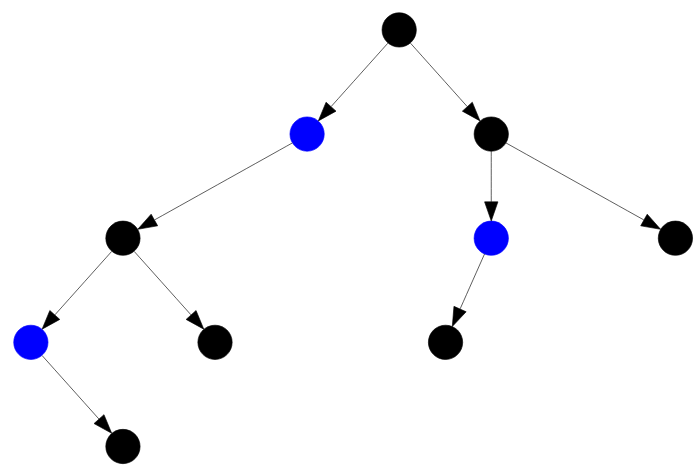
Рисунок — неполные узлы закрашены синим цветом
Вершина, имеющая обоих потомков одновременно, называется полной.
На следующей картинке я обозначу цветом морской волны все полные узлы дерева:
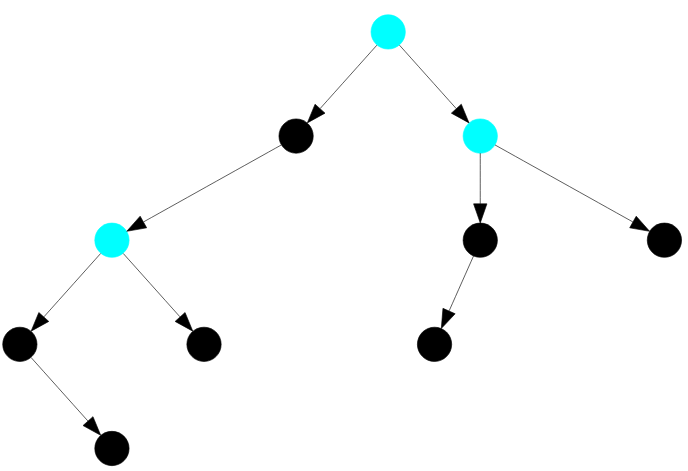
Рисунок — полные узлы закрашены цветом морской волны
➡ Также хочу заметить, что очень желательно правильно обрабатывать «пустой» узел, то есть такой узел, которого физически не существует. С точки зрения памяти такая вершина представляет собой NULL-указатель:
На данный момент выделены следующие виды статуса для узла двоичного дерева:
- пустой ( NULL );
- лист;
- неполный;
- полный.
💡 Но для полноценной работы с вершиной дерева мне этого недостаточно!
Итак, смотрим еще раз на двоичное дерево ( поиска ), в котором синим цветом выделены неполные вершины:

Рисунок — половинчатые узлы бинарного дерева поиска
Я их пронумерую натуральными числами, начиная с $1$ в хаотичном порядке:
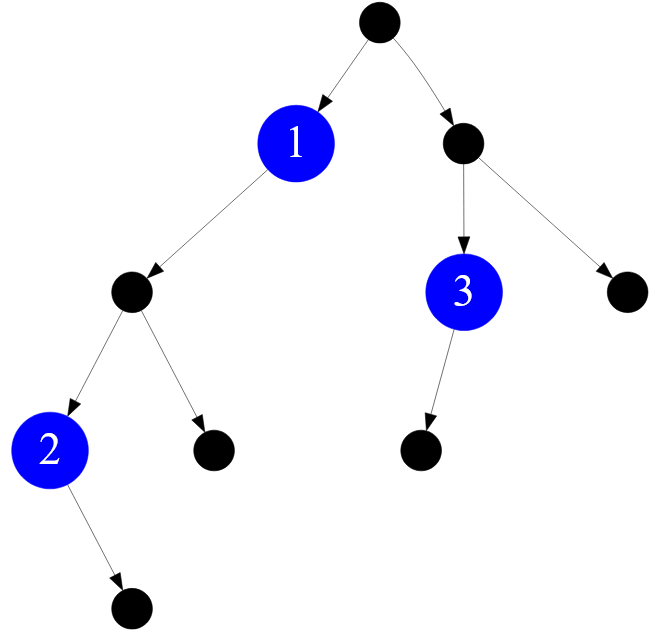
Рисунок — пронумерованные неполные узлы двоичного дерева
С точки зрения типа сыновей ( топологии связей ) узел #$1$ и узел #$3$ идентичны: они имеют только левого потомка. Но при этом узел #$1$ и узел #$2$ неидентичны: эти вершины имеют разного типа потомков — #$1$ — левого, а #$2$ — правого.
➡ Поэтому я хочу сделать дифференциацию неполных узлов в зависимости от того, какого типа потомка ( левого или правого ) они имеют. Это важно в некоторых операциях обработки двоичного дерева поиска, например, при удалении вершины из дерева.
В результате получаем $5$ видов статуса для вершин двоичного дерева ( поиска ):
| # | Тип узла | Расшифровка | В коде |
| $1$ | пустая ( NULL ) | физически не существует | NONE |
| $2$ | листовая | нет ни одного потомка | LEAF |
| $3$ | неполная левая | имеет только левого сына | HALF_LEFT |
| $4$ | неполная правая | имеет только правого сына | HALF_RIGHT |
| $5$ | полная | имеет обоих сыновей | FULL |
➡ Каждый вид статуса чрезвычайно важен при работе с узлами дерева.
На данный момент у меня все готово, чтобы запрограммировать функцию, которая определяет статус заданной вершины бинарного дерева ( поиска ).
Начинаю с декларации перечисления видов статуса:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
//------------------------------------------------------------------------------ // статус узла бинарного дерева поиска //------------------------------------------------------------------------------ typedef enum Node_status { NONE, // нет узла ( NULL-указатель ) LEAF, // пустой ( лист - не имеет сыновей ) HALF_LEFT, // неполный ( имеет только левого сына ) HALF_RIGHT, // неполный ( имеет только правого сына ) FULL // полный ( имеет обоих сыновей ) } Node_status; //------------------------------------------------------------------------------ |
А сама функция будет такой:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
//------------------------------------------------------------------------------ // определение статуса заданного узла: // NONE - NULL ( нет узла ) // LEAF - лист ( нет ни одного потомка ) // HALF_LEFT - неполный узел, имеющий левого сына // HALF_RIGTH - неполный узел, имеющий правого сына // FULL - полный узел ( есть оба сына ) // node - указатель на проверяемый узел // в качестве ответа возвращается статус проверяемого узла дерева //------------------------------------------------------------------------------ Node_status Get_node_status( const Node* const node ) { // проверка на NULL if ( node == NULL ) { return NONE; } // проверка на лист ( нет ни одного сына ) if ( ( node -> left == NULL ) and ( node -> right == NULL ) ) { return LEAF; } // проверка на неполный узел ( левый сын есть, справа NULL ) if ( ( node -> left != NULL ) and ( node -> right == NULL ) ) { return HALF_LEFT; } // проверка на неполный узел ( слева NULL, правый сын есть ) if ( ( node -> left == NULL ) and ( node -> right != NULL ) ) { return HALF_RIGHT; } // остается лишь полный узел ( имеет обоих сыновей ) return FULL; } //------------------------------------------------------------------------------ |
В своих программных реализациях повсеместно использую функцию Get_node_status() и считаю эту функцию крайне полезной. В этой функции решил выбрать именно такой вариант оформления проверок if ( без вложений ).
➡ Пишите в комментариях, насколько предложенная функция определения статуса вершины двоичного дерева кажется полезной и актуальной. А также напишите, как вы на практике в своих программах определяете статус вершины ( скорее всего, используя постоянные проверки if, или все-таки нет ).
| ВНИМАНИЕ | Для заказа программы на двоичное дерево ( поиска ) пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий