Содержание
| ВНИМАНИЕ |
Для заказа программы на графы любой сложности пишите на мой электронный адрес proglabs@mail.ru |
Матрица смежности для представления неориентированного графа
Например, на листке бумаге нарисован такой помеченный ( натуральными числами ) неориентированный невзвешенный граф, состоящий из $6$ вершин:
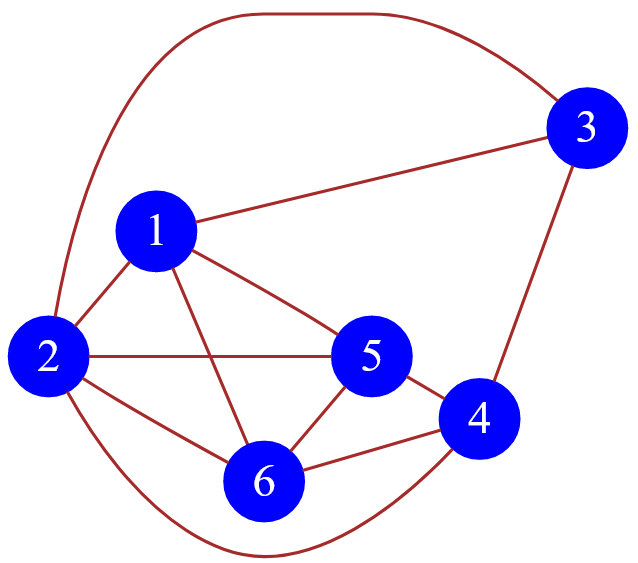
Рисунок — помеченный неориентированный граф, состоящий из $6$ вершин
Возникает закономерный вопрос: каким образом оцифровать этот «аналоговый» граф, чтобы информацию о нем можно было использовать в разного рода вычислениях и кодах программ?
Например, так:
| метки | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ |
| $1$ | $0$ | $1$ | $1$ | $0$ | $1$ | $1$ |
| $2$ | $1$ | $0$ | $1$ | $1$ | $1$ | $1$ |
| $3$ | $1$ | $1$ | $0$ | $1$ | $0$ | $0$ |
| $4$ | $0$ | $1$ | $1$ | $0$ | $1$ | $1$ |
| $5$ | $1$ | $1$ | $0$ | $1$ | $0$ | $1$ |
| $6$ | $1$ | $1$ | $0$ | $1$ | $1$ | $0$ |
Такая матрица порядка $n$ ( $n$ — количество вершин анализируемого графа ), состоящая из $0$ и $1$, называется матрицей смежности неориентированного графа.
➡ Очевидно, что значение $0$ ставится на пересечении тех вершин ( их меток ), которые являются несмежными. Например, это вершины с метками $3$ и $5$.
➡ Очевидно, что значение $1$ ставится на пересечении тех вершин ( их меток ), которые являются смежными ( соседствующими ). Например, это вершины с метками $2$ и $6$.
Так как текущий граф неориентированный, значит, связи между вершинами двусторонние, то есть, если вершина $2$ связана с вершиной $6$, то, предполагается и обратное.
💡 Следовательно, матрица смежности неориентированных графов всегда будет симметричной относительной элементов ее главной диагонали.
Допустим, задан такой нуль-граф $O_1$ ( состоит из одной вершины и не имеет ребер ):

Соответственно его матрица смежности имеет такой вид:
| метки | F |
| F | $0$ |
Допустим, задан такой полный граф $U_4$ ( состоит из $4$-рех вершин и имеет все возможные связи между вершинами ):
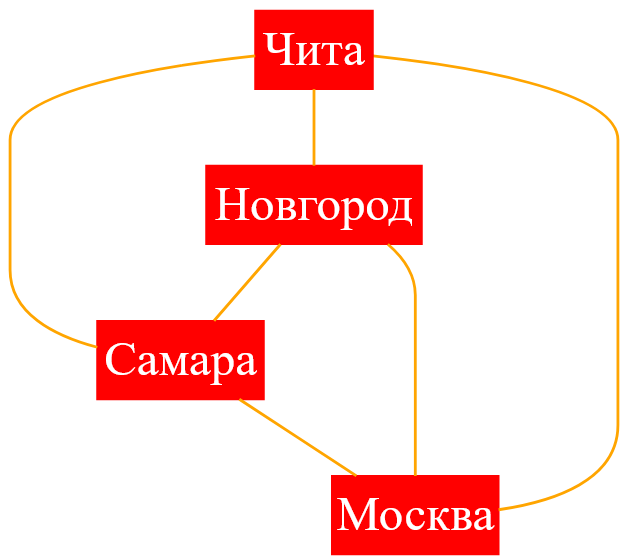
Рисунок — полный граф $U_4$ ( метки вершин — названия городов )
Матрица смежности последнего графа имеет такой вид:
| метки | Москва | Самара | Чита | Новгород |
| Москва | $0$ | $1$ | $1$ | $1$ |
| Самара | $1$ | $0$ | $1$ | $1$ |
| Чита | $1$ | $1$ | $0$ | $1$ |
| Новгород | $1$ | $1$ | $1$ | $0$ |
➡ В матрице смежности полного графа любого порядка в ячейках стоят $1$, кроме элементов главной диагонали. Элементы главной диагонали равны $0$, так как вершина сама с собой никак не связана. О петлях пойдет разговор чуть ниже!
Допустим задан граф, имеющий петлю при вершине с меткой $C$. Этот граф почти является псевдографом.
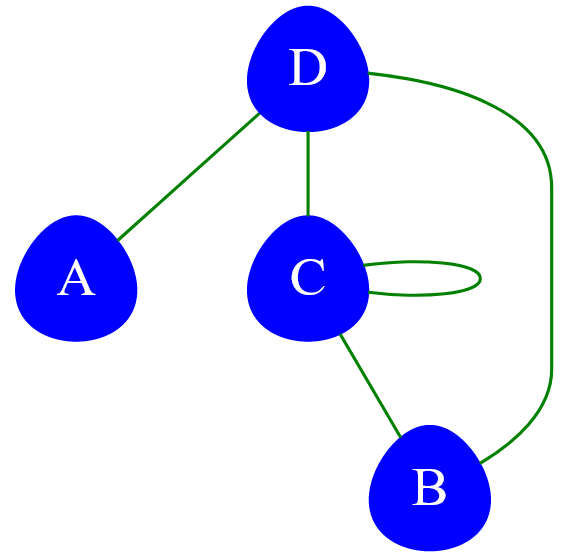
Рисунок — неориентированный граф, имеющий петлю при вершине $C$
Матрица смежности «петлевого» графа имеет вид:
| метки | A | B | C | D |
| A | $0$ | $0$ | $0$ | $1$ |
| B | $0$ | $0$ | $1$ | $1$ |
| C | $0$ | $1$ | $1$ | $1$ |
| D | $1$ | $1$ | $1$ | $0$ |
➡ Если в графе при какой-либо вершине есть петля, то в матрице смежности элементу, стоящему на главной диагонали, соответствующему петлевой вершине, ставится значение, равное $1$.
На практике петли в графе встречаются не так уж и часто.
А теперь рассмотрим классический помеченный неориентированный мультиграф ( метками выступают строковые значения, выражающие названия цветов ):
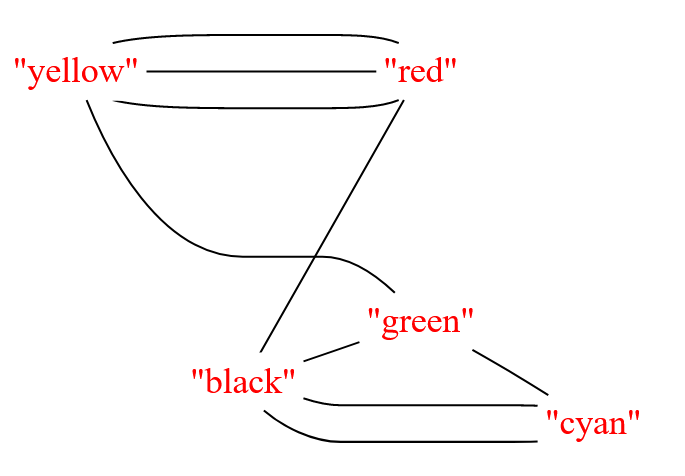
Рисунок — помеченный неориентированный мультиграф ( граф, имеющий кратные ребра )
Видно, что вершины с метками «yellow» и «red» связаны одновременно тремя различными ребрами.
Возникает закономерный вопрос: каким образом в матрице смежности неориентированного мультиграфа учитывать кратные ребра? Очевидно, что поставить $1$ уже недостаточно, так как в этом случае теряется информация о количестве кратных ребер.
➡ В мультиграфных матрицах смежности необходимо ставить количество кратных ребер, соединяющих вершины.
Матрица смежности для приведенного мультиграфа будет иметь такой вид:
| метки | yellow | red | black | green | cyan |
| yellow | $0$ | $3$ | $0$ | $1$ | $0$ |
| red | $3$ | $0$ | $1$ | $0$ | $0$ |
| black | $0$ | $1$ | $0$ | $1$ | $2$ |
| green | $1$ | $0$ | $1$ | $0$ | $1$ |
| cyan | $0$ | $0$ | $2$ | $1$ | $0$ |
Матрица смежности для представления ориентированного графа
💡 Матрицы смежности ориентированных и неориентированных графов очень сильно похожи. Методика заполнения этих матриц почти идентичная. Единственное отличие — надо учитывать направление связей между вершинами ( дуг ).
Рассмотрим ориентированный невзвешенный граф, состоящий из $6$ вершин ( раньше он был неориентированным, но я превратил его в ориентированный, заменив ребра на дуги ):
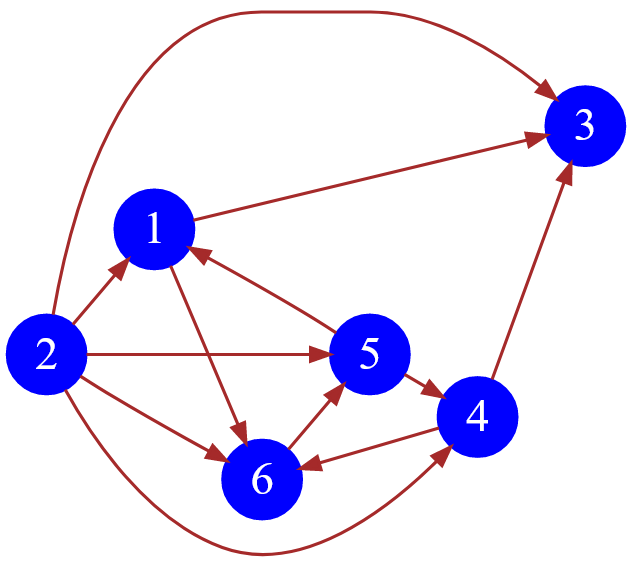
Рисунок — помеченный ориентированный граф, состоящий из $6$ вершин
Матрица смежности текущего графа имеет такой вид:
| метки | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ |
| $1$ | $0$ | $0$ | $1$ | $0$ | $0$ | $1$ |
| $2$ | $1$ | $0$ | $1$ | $1$ | $1$ | $1$ |
| $3$ | $0$ | $0$ | $0$ | $0$ | $0$ | $0$ |
| $4$ | $0$ | $0$ | $1$ | $0$ | $0$ | $1$ |
| $5$ | $1$ | $0$ | $0$ | $1$ | $0$ | $0$ |
| $6$ | $0$ | $0$ | $0$ | $0$ | $1$ | $0$ |
Такая матрица порядка $n$ ( $n$ — количество вершин анализируемого графа ), состоящая из $0$ и $1$, называется матрицей смежности ориентированного графа.
➡ Ячейки матрицы смежности заполняются по следующему правилу: если из некоторой вершины $x$ в вершину $y$ входит дуга, то в соответствующую ячейку вписывается $1$, если дуга не входит — $0$.
Так как текущий граф ориентированный, значит, связи между вершинами односторонние, то есть, если вершина $2$ связана с вершиной $6$, то, обратное не предполагается.
💡 Следовательно, матрица смежности ориентированных графов не будет симметричной относительной элементов ее главной диагонали.
Допустим задан орграф следующей топологии:
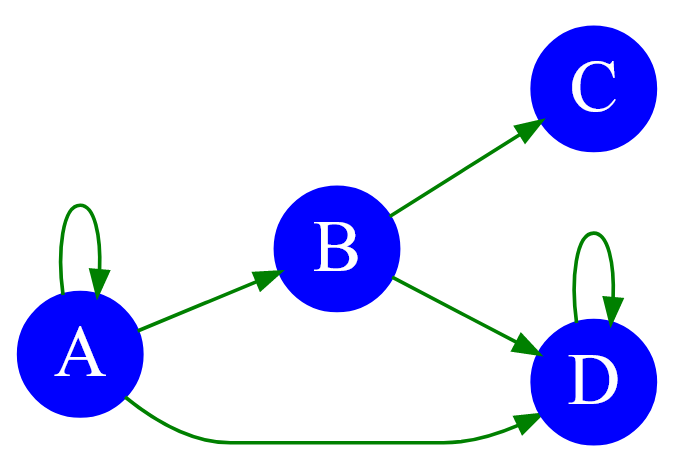
Рисунок — ориентированный граф, имеющий петли при вершинах $A$ и $D$
Матрица смежности «петлевого» графа имеет вид:
| метки | A | B | C | D |
| A | $1$ | $1$ | $0$ | $1$ |
| B | $0$ | $0$ | $1$ | $1$ |
| C | $0$ | $0$ | $0$ | $0$ |
| D | $1$ | $0$ | $0$ | $0$ |
А теперь рассмотрим классический помеченный ориентированный мультиграф ( метками выступают строковые значения, выражающие названия цветов ):

Рисунок — помеченный ориентированный мультиграф ( граф, имеющий кратные ребра )
➡ В мультиграфных матрицах смежности необходимо ставить количество кратных ребер, соединяющих вершины.
Матрица смежности для приведенного ориентированного мультиграфа будет иметь такой вид:
| метки | yellow | red | black | green | cyan |
| yellow | $0$ | $1$ | $0$ | $0$ | $0$ |
| red | $2$ | $0$ | $1$ | $0$ | $0$ |
| black | $0$ | $0$ | $0$ | $0$ | $0$ |
| green | $1$ | $0$ | $1$ | $0$ | $0$ |
| cyan | $0$ | $0$ | $2$ | $1$ | $0$ |
В каких случаях для неориентированного и ориентированного графов их матрицы смежности совпадают?
Хочу показать вам два графа ( в принципе, можно считать, что эти графы являются изоморфными ).
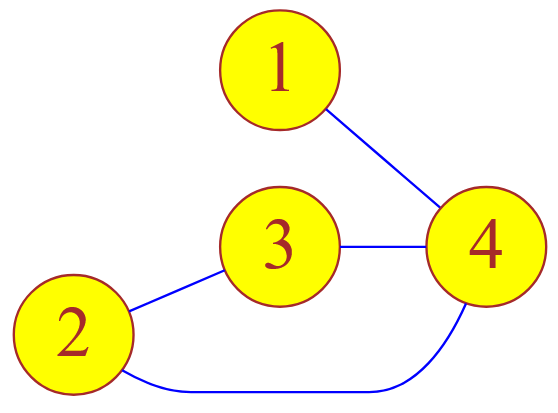
Рисунок — помеченный неориентированный граф, состоящий из $4$ вершин
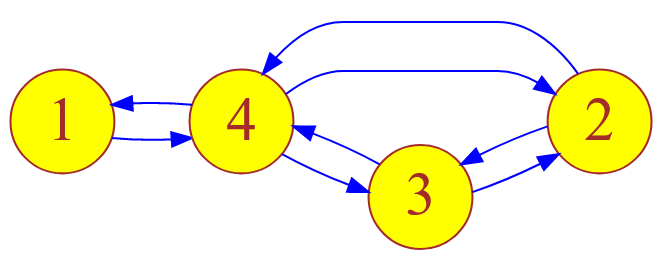
Рисунок — помеченный ориентированный граф, состоящий из $4$ вершин
Матрицы смежности представленных графов совпадают между собой на $100\%$ и имеют такой вид:
| метки | 1 | 2 | 3 | 4 |
| 1 | $0$ | $0$ | $0$ | $1$ |
| 2 | $0$ | $0$ | $1$ | $1$ |
| 3 | $0$ | $1$ | $0$ | $1$ |
| 4 | $1$ | $1$ | $1$ | $0$ |
➡ Из этого вытекает некоторое умозаключение: любой неориентированный граф можно представить в форме ориентированного графа, заменив каждое ребро на две разнонаправленных дуги. Обратное утверждение не имеет силы.
Где применяют графовые матрицы смежности
Матрицы смежности нашли широчайшее применение во множестве графовых алгоритмов. Я лишь перечислю малую толику из этих алгоритмов:
➡ алгоритм Дейкстры ( нахождение кратчайшего пути от заданной вершины до всех остальных );
➡ теоремы Оре и Дирака ( достаточные условия проверки графа на «гамильтоновость» ).
Структуры данных, при помощи которых описывают матрицы смежности в программах
Выше ( в этой статье ) я приводил множество примеров графовых матриц смежностей. Математически все они представляли собой матрицы $n$-го порядка, где $n$ — количество вершин заданного графа.
💡 С точки зрения программных структур данных эти матрицы можно описывать целочисленными динамическими двухмерными массивами.
Пример объявления матрицы смежности на языке «чистый» Си:
|
1 |
int** matrix = NULL; |
После этого в программе будет выделена динамическая память и заполнена матрица.
Работать с двухмерным массивом в программе крайне удобно и просто. Достаточно, например, используя цикл со счетчиком ( цикл for ), сканировать матрицу смежности построчно/поколончато, вычисляя нужную информацию.
Если информация о графе статичная, то есть известна заранее, плюс она не меняется в процессе выполнения программы, то, зачастую, матрицу смежности инициализирует при ее объявлении. В таких случаях матрицу смежности описывают статичным ( автоматическим ) двухмерным массивом.
Для такого неориентированного графа:
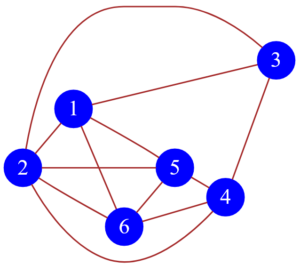
Рисунок — помеченный неориентированный граф, состоящий из $6$ вершин
Матрицу смежности можно объявить и проинициализировать в программе так:
|
1 2 3 4 5 6 7 8 9 10 |
// фиксированная матрица смежности неориентированного графа const int matrix[ VERTEX_COUNT ][ VERTEX_COUNT ] = { 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0 }; |
➡ Пишите в комментариях, что непонятно по графовым матрицам смежности. Если у вас есть какой-то граф, для которого визуально нужно построить матрицу смежности, то расскажите об этом.
| ВНИМАНИЕ |
Для заказа программы на графы любой сложности или записи на подготовку пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий