| ВНИМАНИЕ |
Для заказа программирования высшей математики пишите на мой электронный адрес proglabs@mail.ru |
У меня студенты очень часто заказывают лабораторные работы, связанные с программированием высшей математики. Поэтому решил написать эту статью-шпаргалку, в которой поясню, как использовать метод деления отрезка пополам при приближенном нахождении корня уравнения.
➡ Сразу отмечу, что метод бисекции находит приближенное значение корня некоторого нелинейного уравнения.
Уравнение вида $k \cdot x + b = 0$, где $k,\ b$ — действительные числа, называется линейным. Следовательно, любые уравнения другого вида можно считать нелинейными.
➡ Также нужно помнить, что метод за один запуск может найти с заданной точностью какой-то один корень. Если уравнение имеет несколько корней, например, $3$ штуки, то для нахождения их всех метод бисекции нужно запускать минимум $3$ раза.
Рассмотрю алгоритм в общем виде. Например, задано некое нелинейное уравнение $f(x) = 0$. Моя цель — найти хотя бы один корень этого уравнения, используя метод деления отрезка пополам.
Рассмотрю функцию $y = f(x)$ и построю ее график в прямоугольной системе координат.
💡 График мне нужен, чтобы отделить корень на некотором, достаточно малом отрезке $[a;\ b]$.
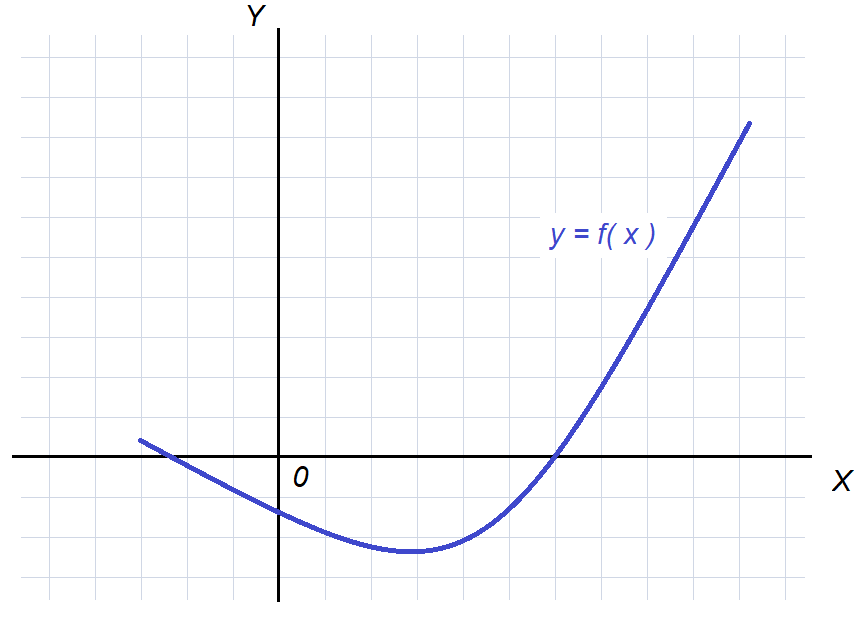
Рисунок — график заданной функции $y = f(x)$ в общем виде
Из графика видно, что он пересекает ось абсцисс $2$ раза, следовательно, исследуемое нелинейное уравнение $f(x) = 0$ имеет $2$ различных корня.
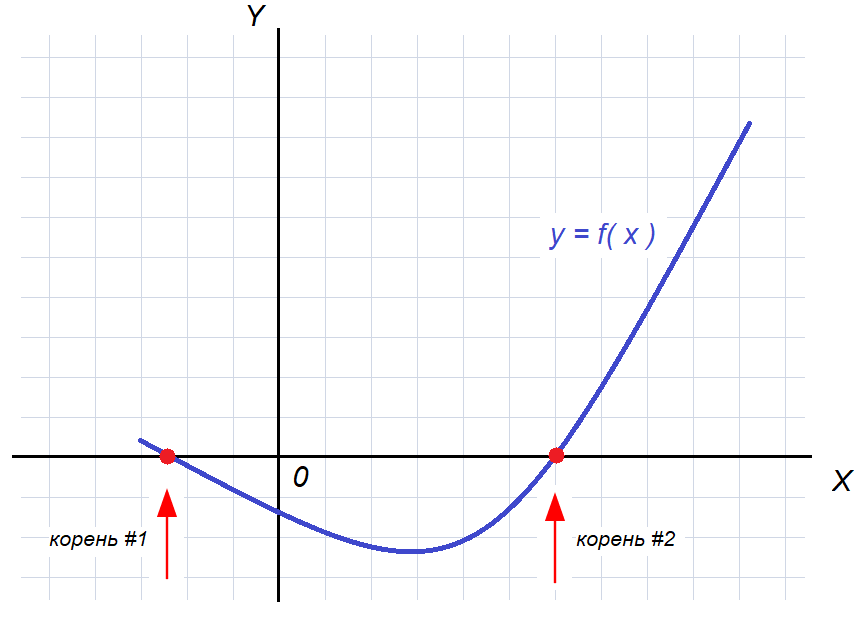
Рисунок — график функции пересекает ось $Ox$ в двух точках
Я планирую поработать с корнем #2.
➡ То есть перед тем, как непосредственно запускать метод бисекции, приходится проводить подобную графоаналитическую работу.
Мне надо взять такой отрезок на оси абсцисс, который содержит корень #2. Если этого не сделать ( или сделать неправильно ), то метод деления отрезка пополам не сработает так, как надо.
Допустим выбрали такой отрезок $[a;\ b]$:
![этап отделения корня. Отрезок $[a;\ b]$ содержит корень #2](http://www.algograph.ru/wp-content/uploads/videoege/Математический-анализ/page-116/image-3.png)
Рисунок — этап отделения корня. Отрезок $[a;\ b]$ содержит корень #2
➡ Вся работа метода деления отрезка пополам будет происходит в рамках этого отрезка $[a;\ b]$. Поэтому очень важно, чтобы заданная функция $y = f(x)$ была непрерывна на этом отрезке.
Итак, для отделения корня нужно выбрать такой отрезок, на котором анализируемая функция существует в любой точке этого отрезка. В данной статье я выбрал графоаналитический способ, но существуют и другие, например, через взятие производной. Не существует однозначного правила, как наиболее эффективно выбрать нужный отрезок для метода бисекции. Эта проблема ложится на плечи решающего. Поэтому будьте готовы к тому, что вам придется постоянно решать эту проблему, когда применяете метод деления отрезка пополам.
Итак, на выбранном отрезке $[a;\ b]$, рассматриваемая функция $y = f(x)$ непрерывна. Посмотрим на знак значений функции на концах отрезка, то есть посмотрим знак значений $f(a)$ и $f(b)$.
![смотрим на значение функции на концах отрезка $[a;\ b]$](http://www.algograph.ru/wp-content/uploads/videoege/Математический-анализ/page-116/image-4.png)
Рисунок — смотрим на значение функции на концах отрезка $[a;\ b]$
➡ Видно, что знаки значений функций на концах отрезка противоположные. Именно это условие гарантирует, что на данном отрезке существует как минимум один ноль функции ( корень уравнения $f(x) = 0$ ).
Проверить тот факт, что знаки значений функций на концах отрезка $[a;\ b]$ противоположные можно через произведение $f(a) \cdot f(b)$. Если это произведение меньше $0$, то знаки противоположные, иначе — одинаковые.
Кстати, хочу напомнить формулу, по которой можно найти координату центра отрезка ( $x_c$ ), заданного координатами своих концов ( $x_l$ и $x_r$ ):
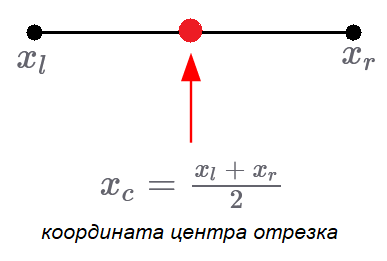
Рисунок — формула для нахождения координаты середины отрезка
Сейчас найду середину отрезка $[a;\ b]$, обозначив его буквой $c$. Также сразу обозначу знак функции в этой точке, то есть знак значения $f(c)$:
![нахождение центра отрезка $[a;\ b]$ и определение знака функции в этой точке](http://www.algograph.ru/wp-content/uploads/videoege/Математический-анализ/page-116/image-6.png)
Рисунок — нахождение центра отрезка $[a;\ b]$ и определение знака функции в этой точке
Итак, точка $c$ разбила отрезок $[a;\ b]$ на два подотрезка: $[a;\ c]$ и $[c;\ b]$. Искомый ноль функции лежит на одном из этих подотрезков.
Чтобы отобрать нужный подотрезок ( речь о подотрезке, содержащий искомый корень ), необходимо воспользоваться правилом произведения, о котором писал чуть выше.
Рассмотрим знаки следующих произведений:
$f(a) \cdot f(c) > 0$
$f(c) \cdot f(b) < 0$
➡ Как было ранее доказано, корень лежит на том отрезке, для которого произведение значений функции на концах отрезка меньше $0$. Делаю вывод, что искомый корень принадлежит отрезку $[c;\ b]$. Визуально это подтверждается. Поэтому последующий анализ перекидывается с отрезка $[a;\ b]$ на отрезок $[c;\ b]$.
Сейчас найду середину отрезка $[c;\ b]$, обозначив его буквой $d$. Также сразу обозначу знак функции в этой точке, то есть знак значения $f(d)$:
![нахождение центра отрезка $[c;\ b]$ и определение знака функции в этой точке](http://www.algograph.ru/wp-content/uploads/videoege/Математический-анализ/page-116/image-7.png)
Рисунок — нахождение центра отрезка $[c;\ b]$ и определение знака функции в этой точке
Итак, точка $d$ разбила отрезок $[c;\ b]$ на два подотрезка: $[c;\ d]$ и $[d;\ b]$. Искомый ноль функции лежит на одном из этих подотрезков.
Чтобы отобрать нужный подотрезок ( речь о подотрезке, содержащий искомый корень ), необходимо воспользоваться правилом произведения, о котором писал чуть выше.
Рассмотрим знаки следующих произведений:
$f(c) \cdot f(d) < 0$
$f(d) \cdot f(b) > 0$
➡ Как было ранее доказано, корень лежит на том отрезке, для которого произведение значений функции на концах отрезка меньше $0$. Делаю вывод, что искомый корень принадлежит отрезку $[c;\ d]$. Визуально это подтверждается. Поэтому последующий анализ перекидывается с отрезка $[c;\ b]$ на отрезок $[c;\ d]$.
💡 На каждой итерации длина отрезка, содержащего искомый корень, сокращается вдвое! Именно по этой причине такой метод приближенного нахождения корня называется методом деления отрезка пополам.
Возникает закономерный вопрос: а когда заканчиваются все вычисления?
Очень важно понимать, что значения корня находится приближенно, то есть с некой погрешностью ( в теории программирования это называется точностью расчетов ).
Например, я хочу найти приближенное значение корня с точностью $EPS = 0.001$, то есть с точностью одна тысячная. Это не очень высокая точность, но вполне приемлемая. Это означает, что если значение реального корня уравнения составляет $5.735$, то мое приближенное решение должно находиться на отрезке $[\ 5.735\ -\ 0.001;\ 5.735\ +\ 0.001\ ] = [\ 5.734;\ 5.736\ ]$.
➡ Поэтому стоит прекратить все вычисления, когда длина отрезка, содержащего искомое значение корня, станет $\leq$ заданной точности, то есть $|a — b | \leq EPS$, где $a$ и $b$ — значения концов отрезка.
Но есть еще один важный нюанс, который многие упускают из виду. Как было сказано ранее, при выборе подотрезка, на котором находится корень, вычисляются произведения $f(a) \cdot f(c)$ и $f(c) \cdot f(b)$, где $a$, $b$ — концы текущего отрезка, а $c$ — середина отрезка.
А представим такую ситуацию, что центр отрезка $c$ точно совпал с искомым корнем, то есть $f(c) = 0$. В этом случае оба эти произведения будут равны $0$ и ни одно из условий не выполнится.
Поясню сказанное на следующем графике $f( x ) = x^2 + x — 20$:
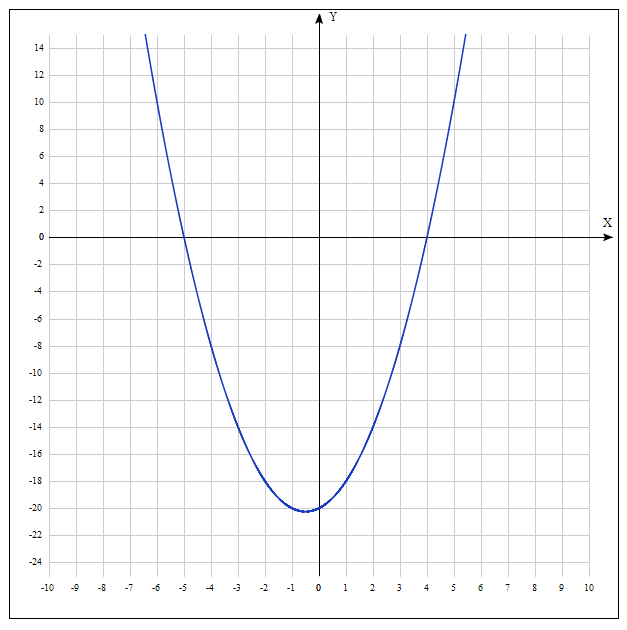
Рисунок — график функции $f( x ) = x^2\ +\ x\ -\ 20$
Очевидно, что уравнение $x^2\ +\ x\ -\ 20$ имеет ровно два целых корня: $-5$ и $4$. Я поработаю с положительным корнем, то есть с корнем $4$ и попробую найти его приближенное значение методом деления отрезка пополам. В качестве стартового отрезка возьму отрезок $[2;\ 6]$.
![поиск корня ( равного $4$ ) на отрезке $[2;\ 6]$](http://www.algograph.ru/wp-content/uploads/videoege/Математический-анализ/page-116/image-9.png)
Рисунок — поиск корня ( равного $4$ ) на отрезке $[2; 6]$
Координата середины отрезка $[2;\ 6]$ равна $4$, то есть $c = 4$. Произведение $f(a) \cdot f(c) = f(2) \cdot f(4) = 0$ и это произведение $f(c) \cdot f(b) = f(4) \cdot f(6) = 0$.
Оба произведения равны $0$. Разумеется, на практике такая ситуация встречается чрезвычайно редко, так как искомые корни далеки от целых значений. Но тем не менее, такая ситуация может возникнуть и моя программа должна корректно ее обрабатывать.
В примере выше я вышел на корень ( его точное значение, равное $4$ ) на самой первой итерации метода деления отрезка пополам. Но при этом длина отрезка, на котором находится корень, составляет $|b\ -\ a| = |6\ -\ 2| = 4$ единицы. Если точность расчетов $EPS = 0.0001$, то метод должен продолжать свою работу, так как все приближенные вычисления по нахождению корня заканчиваются, когда длина подотрезка, содержащего корень, становится $\leq$ заданной точности, то есть должно выполниться такое условие: $|b\ -\ a| \leq EPS$ Да, вот есть такой небольшой неприятный момент в этом методе, на который надо обращать внимание.
➡ Для некоторых нелинейных уравнений метод бисекции не работает, хотя все условия, казалось бы, выполнены.
Рассмотрим функцию $f( x ) = x^2\ -\ 6x\ +\ 9$. Графиком этой функции является парабола, которая касается оси абсцисс лишь в одной точке — точке, с координатами $\{3;\ 0\}$. Другими словами, уравнение $f( x ) = 0$ имеет два одинаковых корня, равных $3$.
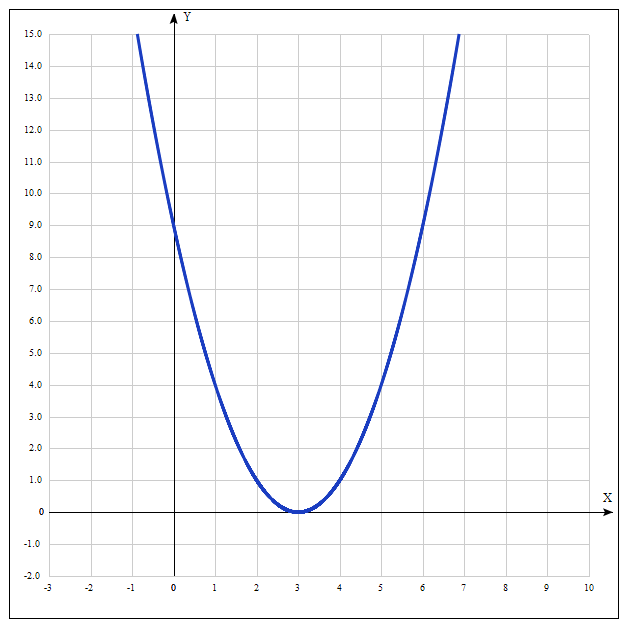
Рисунок — график функции $f( x ) = x^2\ -\ 6x\ +\ 9$
Посмотрим, как себя поведет алгоритм, если попытаться найти приближенное значение корня, равного $3$. Например, возьмем стартовый отрезок $[a;\ b] = [1;\ 6]$.
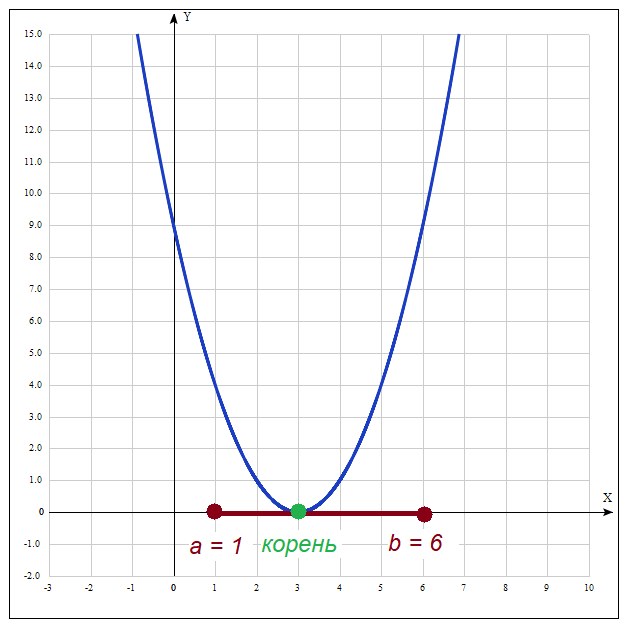
Рисунок — стартовый отрезок для нахождения корня от $1$ до $6$
Значение функции в точке $a = 1$ — положительно. Аналогично значение функции в точке $b = 6$ — также положительно. Следовательно, произведение $f( a ) \cdot f( b )$ будет также положительным. Алгоритм сделает вывод, что на заданном отрезке нет ни одного корня, хотя по факту это не так!
Важный вывод: если график функции касается оси абсцисс, то классический метод деления отрезка пополам начинает работать некорректно.
В результате я написал программу на языке «чистый» Си в среде программирования Visual Studio $2010$ ( стандарт C89 ), которая находит приближенное значение корня заданного нелинейного уравнения. Программа тщательно прокомментирована и учитывает пограничные случаи.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
#include <stdio.h> // ввод-вывод #include <locale.h> // русификация диалогов #include <stdlib.h> // служебные функции #include <math.h> // для работы с модулем ( fabs ) //---------------------------------------------------------------------------------------------------------- // функция, заданная аналитически, для которой определяется приближенное значение корня // F( x ) = x^2 + x - 20 //---------------------------------------------------------------------------------------------------------- double F( const double x ) { return ( x * x + x - 20 ); } //---------------------------------------------------------------------------------------------------------- // нахождение приближенного значения корня уравнения методом деления отрезка пополам ( бисекции ) // a - левая граница отрезка, содержащего искомый корень // b - правая граница отрезка, содержащего искомый корень // изначально предполагается, что отрезок [ a; b ] содержит строго один корень заданного уравнения //---------------------------------------------------------------------------------------------------------- double Bisection( double a, double b ) { // найденный приближенный корень должен отличаться от истинного не более, чем на эту погрешность #define EPS 0.0001 // метод выполняется до тех пор, пока корень, вычисленный на текущей итерации, // не будет отличаться от истинного не более, чем на величину погрешности while ( fabs( b - a ) > EPS ) { // находим середину отрезка [ a; b ] double c = ( a + b ) / 2.0; // нужно понять, на каком подотрезке [ a; c ] или [ c; b ] лежит искомый корень // знаки функций на концах отрезка должны быть различными // если условие выполняется, то искомый корень лежит на отрезке [ a; c ] if ( F( a ) * F( c ) <= 0 ) { b = c; // перестраиваем границы отрезка в формат [ a; b ] } // автоматически иначе искомый корень лежит на отрезке [ c; b ] else { a = c; // перестраиваем границы отрезка в формат [ a; b ] } } // в качестве ответа возвращаем координату центра отрезка [ a; b ], на котором лежит искомый корень // найденное значение приближенного корня гарантировано отличается от истинного не более, чем на величину EPS return ( a + b ) / 2.0; } //---------------------------------------------------------------------------------------------------------- // главная функция ( точка входа ) //---------------------------------------------------------------------------------------------------------- int main( void ) { // границы отрезка, на котором планируется искать приближенное значение корня, методом деления отрезка пополам double a, b; // приближенное значение корня double x; // русификация диалогов программы setlocale( LC_ALL, "Russian" ); // запрашиваем вводом с клавиатуры границы первоначального отрезка [ a; b ] printf( "Введите через пробел 2 числа - границы отрезка [ a; b ]: " ); scanf( "%lf %lf", &a, &b ); // сразу убедимся, что корень лежит внутри заданного отрезка [ a; b ], то есть на интервале ( a; b ) if ( ( F( a ) * F( b ) >= 0 ) ) { printf( "На заданном отрезке [ a; b ] = [ %0.4lf; %0.4lf ] нет корня, либо больше одного корня! Программа прерывается!", a, b ); } else { x = Bisection( a, b ); printf( "\nПриближенное значение корня ( с точностью 0.0001 ) на отрезке [ %0.4lf; %0.4lf ] заданного уравнения: \n\tx = %0.4lf", a, b, x ); } // задержка программы, чтобы у пользователя была возможность просмотреть результат printf( "\n\n" ); EXIT_SUCCESS; } //---------------------------------------------------------------------------------------------------------- |
В программе заложена функция $f( x ) = x^2\ +\ x\ -\ 20$. Уравнение $f( x ) = 0$, как было показано ранее, имеет два различных корня: $-5$ и $4$. Протестируем работу программы, задав границы стартового отрезка $[1.5;\ 7.99]$.

Рисунок — результаты работы программы
Пишите в комментариях, что непонятно в рамках рассмотренного алгоритма нахождения приближенного значения корня методом деления отрезка пополам. Также расскажите, для каких уравнений вам приходилось прибегать к методу бисекции, и, с какими трудностями вы столкнулись.
| ВНИМАНИЕ |
Для заказа программирования высшей математики пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий