Содержание
Описание проблемы
Дана следующая схема дорог, связывающих города. Каждая дорога имеет цену, которую надо заплатить, чтобы по ней проехать.
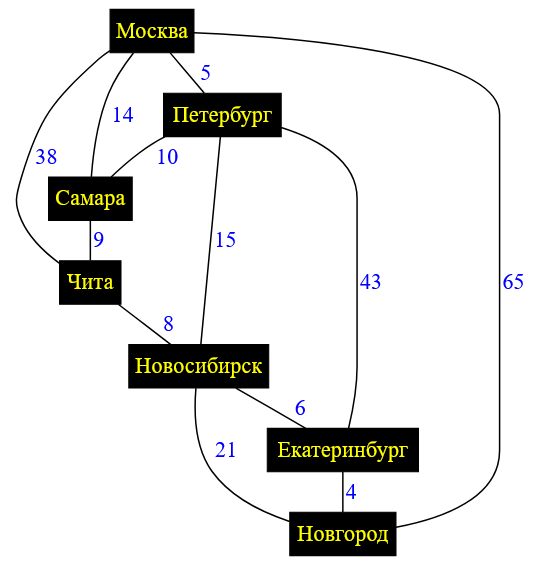
Рисунок — схема дорог, связывающих города
Моя задача — добраться из города Москва до Новгород по минимальной цене.

Рисунок — надо добраться из Москвы до Новгорода по минимальной цене
💡 В решении моей проблемы поможет алгоритм Дейкстры.
Введу следующие ограничения ( допущения, дополнения ):
➡ Города буду называть вершинами ( узлами ).
➡ Дороги, связывающие города буду называть ребрами.
➡ Все дороги двусторонние. Это означает, если можно проехать из Москвы до Самары, то также можно и из Самары до Москвы.
➡ Стоимость проезда по дороге — положительная величина. Почему алгоритм Дейкстры работает некорректно для ребер отрицательного веса — об этом будет написано ниже.
Переформулирую проблему в терминах теории графов: необходимо найти кратчайший путь ( путь минимального веса ) от заданной вершины неориентированного графа до другой заданной вершины.
💡 Классический алгоритм Дейкстры находит кратчайшие пути от заданной вершины до всех остальных вершин графа.
Графический анализ алгоритма Дейкстры
Начальный этап — этап инициализации. До каждого города, кроме стартового, принимается расстояние, равное бесконечности ( $\infty$ ).

Рисунок — расстояние до всех вершин от заданной равно $\infty$
Также я хочу ввести следующие обозначения для статусов вершин ( названий городов ). Эти статусы будет постоянно меняться в процессе работы алгоритма Дейкстры. В качестве примера рассмотрю город Самара.
| Название статуса | Графическое обозначение |
| Непосещенная вершина ( город ) | Самара |
| В процессе обработки | Самара |
| Обработанная вершина ( город ) | Самара |
На этапе инициализации в работу включается стартовая вершина, то есть город Москва, поэтому графическое состояние схемы дорог будет следующим:
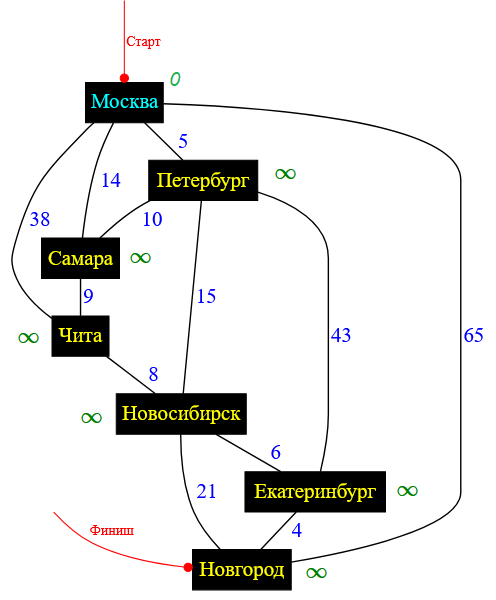
Рисунок — этап инициализации алгоритма Дейкстры
На следующем этапе необходимо выбрать один из городов, имеющих статус «В процессе обработки», но при этом у этого города должна быть минимальная метка стоимости. На данный момент только один город имеет такой статус. Это город Москва. Метка стоимости у этого города равна $0$. Это справедливо, так как добраться до Москвы ничего не стоит, так как изначально мы находимся в Москве.
И сейчас необходимо от этого города ( Москва ) пройти ко всем соседним связанным городам, у которых статус не равен «Обработанная вершина». Москва напрямую связана только с четырьмя городами:
-
- Самара;
- Петербург;
- Чита;
- Новгород.
При этом все эти четыре города имеют статус непосещенных.
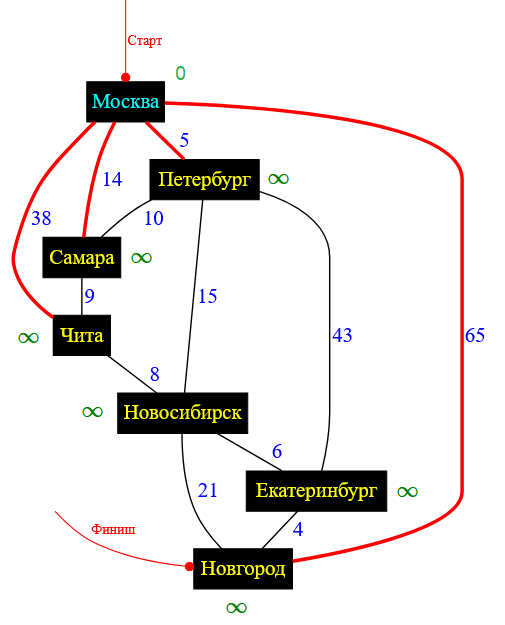
Рисунок — перебор всех городов-соседей для города Москва
➡ В какой последовательности перебирать смежные города? Абсолютно не важно! Можно сначала рассмотреть связь Москва — Самара, а можно Москва — Новгород и т.д. На конечный результат алгоритма Дейкстры это никак не повлияет.
Покажу, какие проверки происходят, когда делается анализ связи, например, Москва — Чита. Текущая ценовая метка у города Чита равна $\infty$. Стоимость проезда между Москвой и Читой составляет $38$. Ценовая метка у города Москва равна $0$. Следовательно, чтобы добраться от Москвы до Читы достаточно потратить $0 + 38 = 38$, а это меньше, чем $\infty$.
💡 Поэтому меняем ценовую метку у города Чита на $38$.
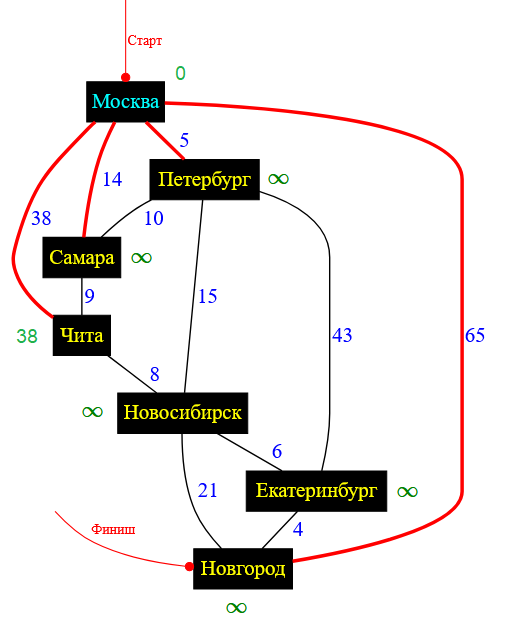
Рисунок — найден более дешевый путь ( $38$ ) от Москвы до Читы
Аналогично пересчитываются весовые метки у Самары, Петербурга и Новгорода.
➡ После этого город Москва считается посещенным и в дальнейших расчетах участия не принимает! А только что пересчитанные города-соседи принимают статус «В работе».
В результате схема дорог принимает такой вид:

Рисунок — схема дорог после обработки города Москва и ее соседей
На следующем этапе необходимо выбрать город, у которого статус «В работе», а также этот город должен иметь наименьшую метку стоимости. На данный момент $4$ города удовлетворяют этому условию. Выпишу их:
| Название города | Стоимость проезда до города |
| Чита | $38$ |
| Самара | $14$ |
| Петербург | $5$ |
| Новгород | $65$ |
➡ Минимальную стоимость проезда имеет Петербург ( $5$ единиц ). Поэтому подвергаю обработке именно этот город по аналогии, как это было сделано с Москвой.
Необходимо от этого города ( Петербург ) пройти ко всем соседним связанным городам, у которых статус не равен «Обработанная вершина». Петербург напрямую связан только с четырьмя городами:
- Москва;
- Самара;
- Новосибирск;
- Екатеринбург.
Но Москва имеет статус «Обработанная вершина», поэтому в вычислениях она участия не принимает. По факту остается лишь $3$ соседа для Петербурга.
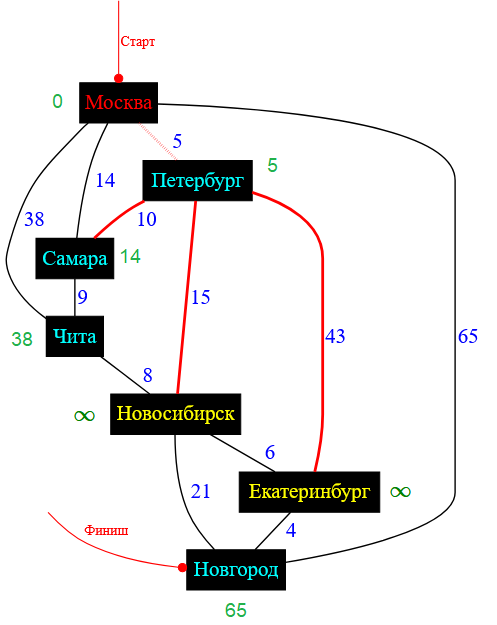
Рисунок — перебор всех городов-соседей для города Петербург
💡 Обращаю особое внимание на пару смежных городов Петербург — Самара. Самара, несмотря на то, что имеет статус «В работе» принимает участие в вычислениях кратчайшего пути.
Пересчитываем стоимости проезда до Самары, Новосибирска и Екатеринбурга. Всем этим городам ставим статус «В работе», а узел-Петербург принимает статус «Обработан» и в дальнейших вычислениях, как и Москва, он уже участие не принимает.
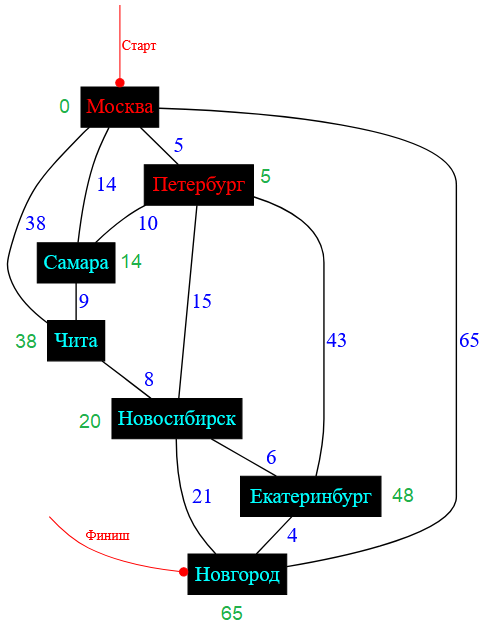
Рисунок — схема дорог после обработки города Петербург и его соседей
На следующем этапе необходимо выбрать город, у которого статус «В работе», а также этот город должен иметь наименьшую метку стоимости. На данный момент $5$ городов удовлетворяют этому условию. Выпишу их:
| Название города | Стоимость проезда до города |
| Чита | $38$ |
| Самара | $14$ |
| Новгород | $65$ |
| Новосибирск |
$20$ |
| Екатеринбург |
$48$ |
➡ Минимальную стоимость проезда имеет Самара ( $14$ единиц ). Поэтому подвергаю обработке именно этот город по аналогии, как это было сделано с Москвой и Петербургом.
Необходимо от этого города ( Самара ) пройти ко всем соседним связанным городам, у которых статус не равен «Обработанная вершина». Самара напрямую связана только с тремя городами:
- Москва;
- Петербург;
- Чита.
Но Москва и Петербург имеет статус «Обработанная вершина», поэтому в вычислениях они участия не принимают. По факту остается лишь $1$ сосед для Самары.
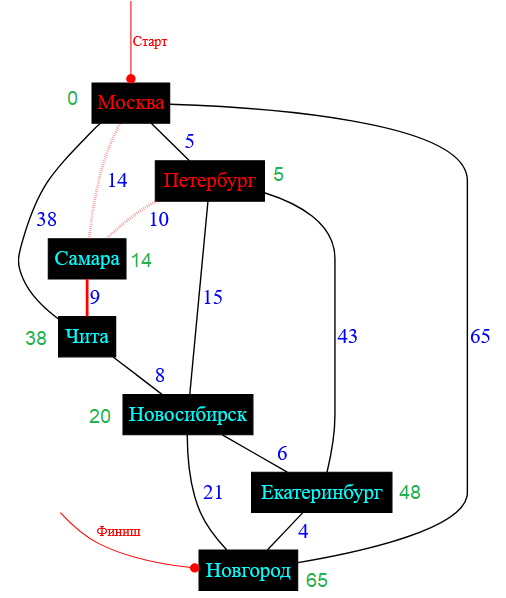
Рисунок — перебор всех городов-соседей для города Самара
Пересчитываю стоимость от Самары до Читы: $14 + 9 = 23 < 38$ — да, следовательно, надо переписать ценовую метку для Читы, а сам город принимает статус «Посещен».
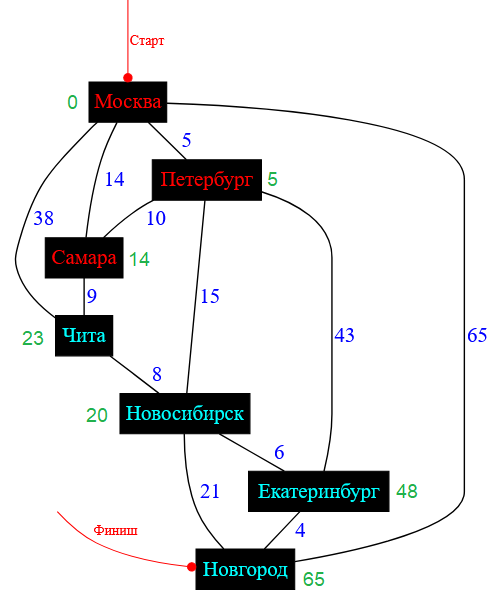
Рисунок — схема дорог после обработки города Самара и ее соседей
На следующем этапе снова выбирается город, имеющий статус «В работе» и минимальную ценовую метку. Это город Новосибирск. Происходит пересчет стоимости пути до его городов-соседей, у которых статус отличен от «Посещен».
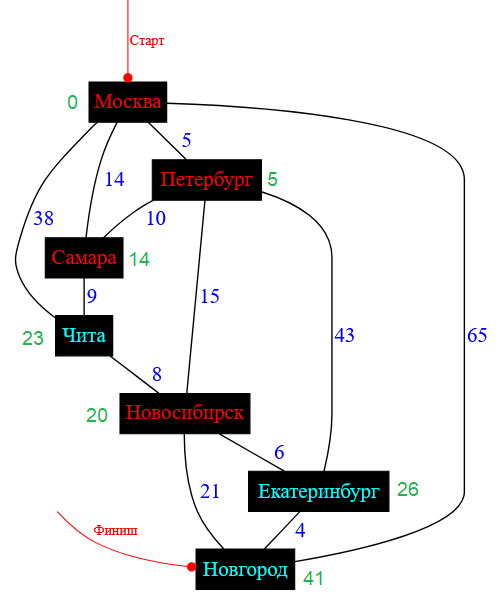
Рисунок — схема дорог после обработки города Новосибирск и его соседей
Сейчас следует пересчитать город Чита ( имеет минимальную ценовую метку, равную $23$ ) и ее возможных соседей. Кстати, все смежные города для Читы уже обработаны ( Самара, Москва, Новосибирск ), поэтому город просто принимает статус «Посещен».

Рисунок — схема дорог после обработки города Чита и ее соседей
Из двух оставшихся необработанных городов берем Екатеринбург, так как его ценовая метка ( $26$ ) меньше, чем у Новгорода ( $41$ ). После пересчета Екатеринбурга получаем следующую картину:
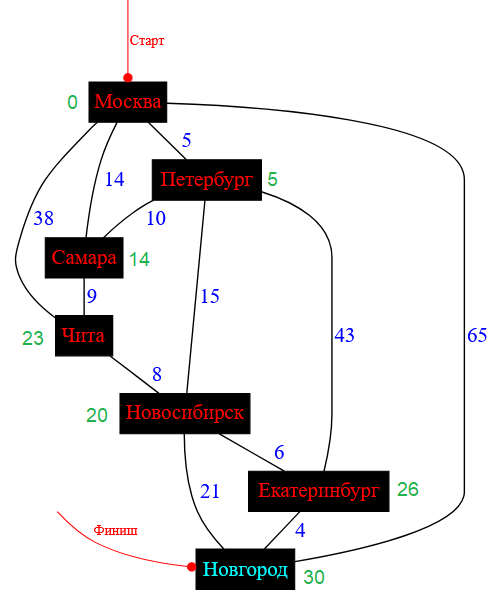
Рисунок — схема дорог после обработки города Екатеринбург и его соседей
И на завершающем этапе пересчитывается последний необработанный город. Это Новгород. Очевидно, что ценовые метки не меняются.
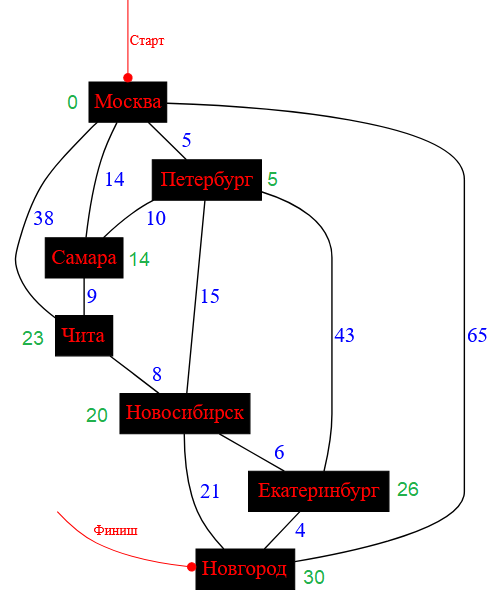
Рисунок — схема дорог после обработки города Новгород и его соседей
В результате у каждого города сформирована минимальная ценовая метка, которая показывает, сколько потребуется заплатить, чтобы добраться от Москвы до этого города:
| # | Город | Минимальная стоимость проезда |
| $1$ | Москва | $0$ |
| $2$ | Петербург | $5$ |
| $3$ | Новосибирск | $20$ |
| $4$ | Самара | $14$ |
| $5$ | Новгород | $30$ |
| $6$ | Чита | $23$ |
| $7$ | Екатеринбург | $26$ |
Мне нужно было узнать, какова минимальная стоимость пути из Москвы в Новгород. Алгоритм Дейкстры дал мне ответ на этот вопрос: придется заплатить $30$ единиц.
Дополнительно можно еще посмотреть сам маршрут ( кратчайший путь ) из Москвы в Новгород:
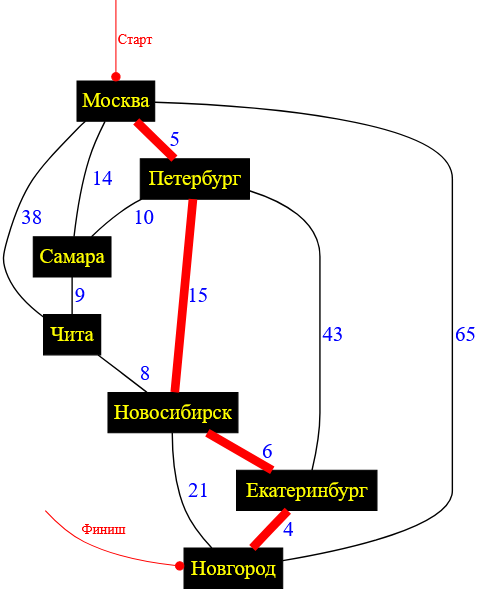
Рисунок — кратчайший путь ( минимальный по цене ) из Москвы в Новгород
Маршрут минимальной стоимости: Москва — Петербург — Новосибирск — Екатеринбург — Новгород. Маршрут состоит из $5$ городов и его стоимость $30$ единиц.
💡 Вообще, задача классического алгоритма Дейкстры — нахождение кратчайших путей от заданной вершины до всех остальных. Речи не идет о том, чтобы восстановить сам этот минимальный путь. Но, как правило, это нужно уметь делать. И я покажу, как получить сам кратчайший путь ( перечислением посещенных вершин ), но чуть позже, когда пойдет детальный анализ структур данных.
Почему алгоритм Дейкстры не работает на графах, имеющих ребра отрицательного веса
➡ Это очень популярный вопрос на все возможных программистских форумах и, в том числе, от моих учеников.
Для этого я рассмотрю небольшой неориентированный взвешенный граф, состоящий буквально из $4$ вершин. Одно из ребер будет иметь отрицательный вес.
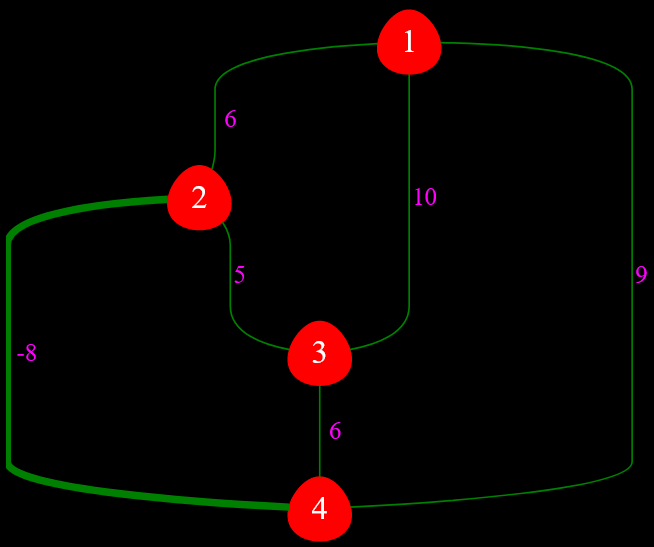
Рисунок — неориентированный взвешенный граф, имеющий одно ребро отрицательного веса, для алгоритма Дейкстры
➡ Ребро между вершинами $2$ и $4$ имеет отрицательный вес, равный $-8$.
Например, я попробую найти кратчайший путь между вершинами $3$ и $1$. Очевидно, для реализации задуманного, мне нужно будет запустить алгоритм Дейкстры от вершины $3$.
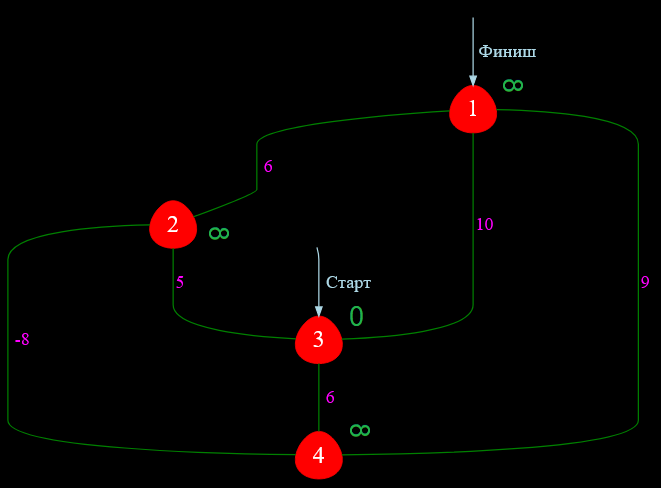
Рисунок — инициализация вершин графа перед запуском алгоритма Дейкстры
После обработки стартовой вершины ( под номером $3$ ) получим такое состояние графа:
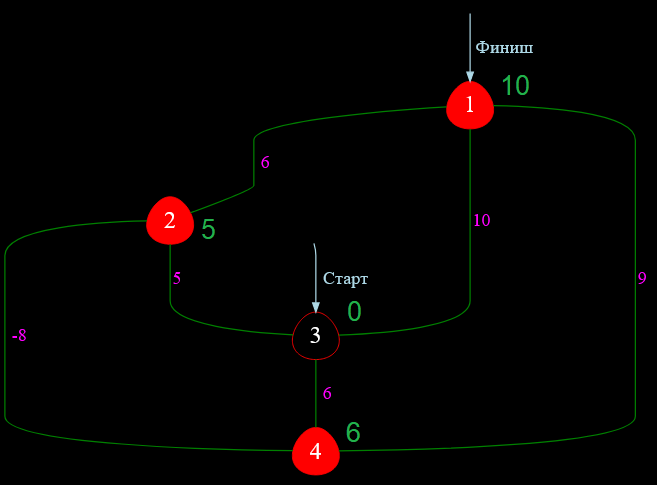
Рисунок — состояние графа после обработки вершины $3$
Среди вершин, имеющих статус «В работе», вершина номер $2$ имеет наименьшую ценовую метку, равную $5$. Поэтому обрабатываю теперь вершину $2$ и получаю:
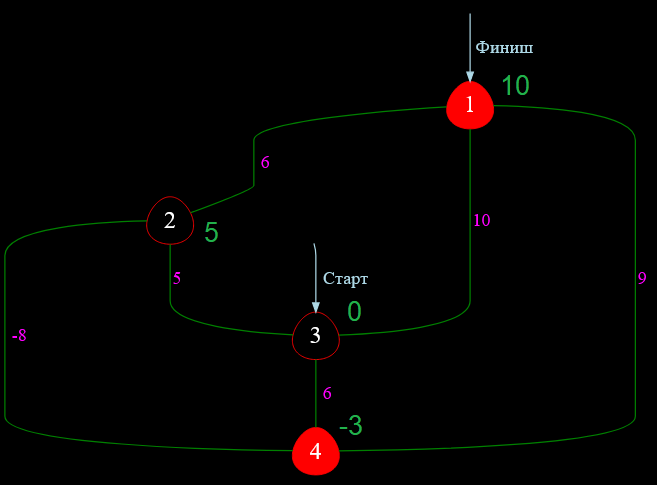
Рисунок — состояние графа после обработки вершины $2$
Среди вершин, имеющих статус «В работе», вершина номер $4$ имеет наименьшую ценовую метку, равную $-3$. Поэтому обрабатываю теперь вершину $4$.
💡 Но есть нюанс! В соответствии с алгоритмом Дейкстры вершины $2$ и $3$ уже обработаны и в последующих вычислениях участия не принимают. То есть получается, что кратчайший путь от вершины $3$ до вершины $2$ составляет $5$ единиц. Но разве это справедливо?! Очевидно, если прокладывать маршрут к вершине $2$ через $4$, то его протяженность составит $6 + ( -8 ) = -2$ ед. А значение $-2$ математически меньше, чем $+5$. Следовательно, алгоритм Дейкстры некорректно рассчитал расстояние от стартового узла графа ( от узла $3$ ) до узла $2$.
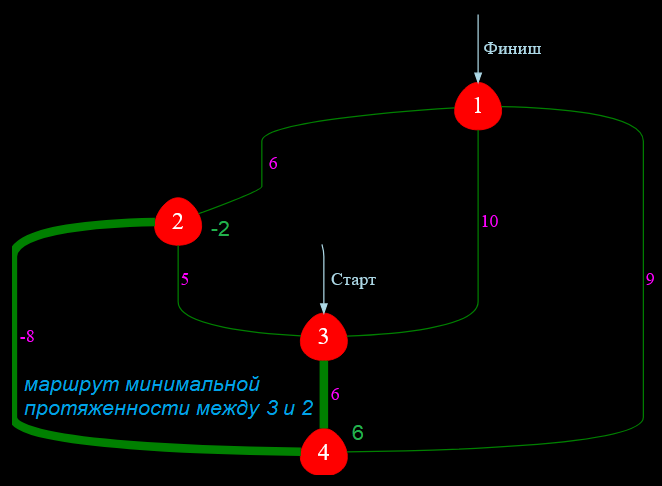
Рисунок — правильный маршрут минимальной протяженности между вершинами $3$ и $2$
Другими словами, вершина $2$ «не знала», что от вершины $4$ найдется ребро, которое пересчитает расстояние до $2$ в сторону уменьшения. При положительных весах это невозможно, а вот отрицательные весовые значения нарушают это правило.
➡ По этой причине алгоритм Дейкстры некорректно работает, когда граф имеет отрицательные ребра.
Но есть еще нюанс! На рассматриваемом графе элементы $2$ и $4$ соединяет ребро отрицательного веса. По факту эти вершины образуют цикл отрицательного веса. Из этого следует, что можно до бесконечности «прыгать» между этими вершинами постепенно уменьшая длину маршрута.
Лично я запомнил раз и навсегда: если нужен алгоритм Дейкстры, то необходимо запрещать отрицательные веса в графе. Иначе результат будет непредсказуем ( а по факту — неправилен ).
Структуры данных для алгоритма Дейкстры
Очень важно понять, какие структуры данных нужны для решения. Правильный выбор структур данных не менее важен, чем правильный выбор алгоритма решения задачи. Как правило, новички, очень мало времени уделяют проработке структур данных и получают в процессе кодирования лютые проблемы.
Покажу, какие структуры данных мне потребуется, чтобы «наложить» алгоритм Дейкстры на эту схему дорог:

Рисунок — схема дорог, связывающих города
Формат входных данных
Существует $4$ фундаментальных формата входных данных:
- ввод с клавиатуры;
- считывание из заданного текстового/двоичного файла;
- случайная генерация;
- по формуле.
➡ Вводить с клавиатуры постоянно названия всех городов и стоимость проезда между ними утомительно. Перед каждым запуском программы придется проводить практически один и тот же ввод. Этот вариант отбросим.
➡ Случайно генерировать данные достаточно неудобно. Нужно иметь мощную базу городов, которую где-то нужно хранить. В целом этот вариант приемлем, но его также отбросим.
➡ Формульный ввод. Для задания графов этот вариант практически неприменим. Отбрасываем.
💡 Считывать информацию о городах и весах ребер из текстового файла удобно. Также эту информацию легко редактировать. Поэтому я выбираю именно этот формат входных данных!
Для рассматриваемой схемы дорог входной текстовый файл будет иметь вид:
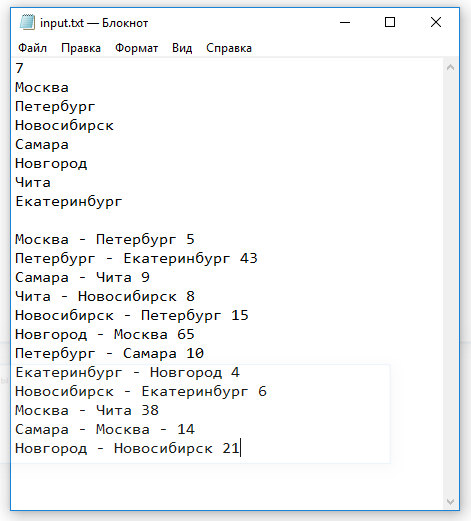
Рисунок — входной текстовый файл с данными для алгоритма Дейкстры
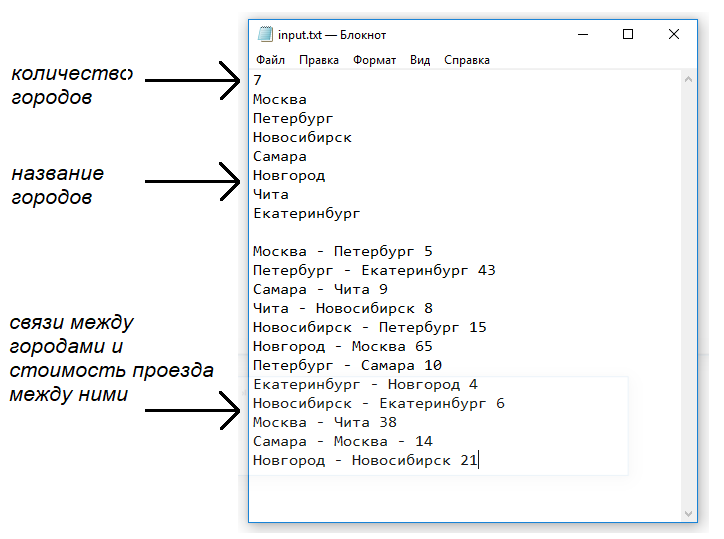
Рисунок — входной текстовый файл состоит из $3$ блоков данных
Где хранить информацию о городах
Во-первых, перед тем, как запускать на выполнение алгоритм Дейкстры, необходимо знать количество вершин графа. То есть число узлов графа должно быть известно. В моем примере $7$ вершин, имеющих следующие метки:
| Номер вершины | Метка вершины |
| $0$ | Москва |
| $1$ | Петербург |
| $2$ | Новосибирск |
| $3$ | Самара |
| $4$ | Новгород |
| $5$ | Чита |
| $6$ | Екатеринбург |
➡ Нумерацию вершин графа я неспроста взял от $0$. Это связано с тем, что в языке «чистый» Си первый элемент любого одномерного массива имеет индекс, равный $0$.
То есть в программе у меня будет специальный массив, состоящий из $7$ элементов. А значениями элементов этого массива будет информация о городах.
Каждый город ( вершина графа ) должна включать такую полезную информацию:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
//--------------------------------------------------------------------------------------- // описание статуса вершины графа // в процессе работы алгоритма Дейкстры любая вершина графа может принимать 3 состояния: // 1. быть непосещенной // 2. быть в работе // 3. быть посещенной //--------------------------------------------------------------------------------------- typedef enum Status { UNVISITED, WORK, VISITED } Status; //--------------------------------------------------------------------------------------- // описание сущности "Вершина графа" //--------------------------------------------------------------------------------------- typedef struct Vertex { char* name; // метка ( название города ) int distance; // длина кратчайшего пути до вершины от заданной Status status; // статус int from; // показывает индекс вершины, из которой можно попасть в текущую вершину } Vertex; //--------------------------------------------------------------------------------------- |
А вот, собственно, одномерный массив вершин графа:
|
1 2 |
// массив городов ( вершин графа ) Vertex* vertexes = NULL; |
Где хранить информацию о дорогах между городами и стоимости проезда по ним
Это не самый легкий момент в проектировании. Есть много разных способов. Я выберу наиболее простой и понятный вариант — задействую весовую матрицу.
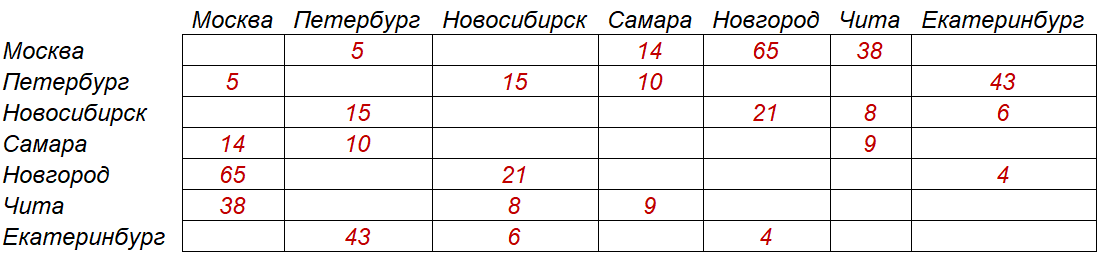
Рисунок — весовая матрица заданного графа
➡ Можно говорить, что заданный граф я отражаю в весовую матрицу. Иногда удобнее отражать граф в список смежности и т.д.
Реализация алгоритма Дейкстры на языке Си
Приведу полный код программы, который выполняет следующие действия:
➡ считывание данных из заданного текстового файла;
➡ поиск кратчайших путей от заданное вершины графа до всех остальных, используя алгоритм Дейкстры;
➡ вывод результата в понятной форме.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 |
#include <stdio.h> // ввод-вывод #include <stdlib.h> // служебные функции #include <locale.h> // русификация диалогов #include <string.h> // для строк ( char* ) #include <iso646.h> // для and / or #include <crtdbg.h> // проверка утечек памяти //--------------------------------------------------------------------------------------- // описание статуса вершины графа // в процессе работы алгоритма Дейкстры любая вершина графа может принимать 3 состояния: // 1. быть непосещенной // 2. быть в работе // 3. быть посещенной //--------------------------------------------------------------------------------------- typedef enum Status { UNVISITED, WORK, VISITED } Status; //--------------------------------------------------------------------------------------- // описание сущности "Вершина графа" //--------------------------------------------------------------------------------------- typedef struct Vertex { char* name; // метка ( название города ) int distance; // длина кратчайшего пути до вершины от заданной Status status; // статус int from; // показывает индекс вершины, из которой можно попасть в текущую вершину } Vertex; // прототипы функций int Get_vertexes_count_from_text_file( const char* const ); Vertex* Read_name_towns_from_text_file( const char* const , const int ); int** Read_weight_from_text_file( const Vertex* const , const int , const char* const ); int Get_index_vertex_by_name_town( const Vertex* const , const int , const char* const ); int Get_index_next_work_vertex( const Vertex* const , const int ); void Dijkstra( Vertex* const vertexes, const int , const int** const , const int ); void Print_path( const Vertex* const , const int , const int ); Vertex* Delete_vertexes( Vertex* , const int ); int** Delete_matrix( int** , const int ); //--------------------------------------------------------------------------------------- // считывание из входного текстового файла с именем name_file количество городов ( вершин ) //--------------------------------------------------------------------------------------- int Get_vertexes_count_from_text_file( const char* const name_file ) { int n; FILE* f; char buf[ BUFSIZ ]; f = fopen( name_file, "r" ); fgets( buf, BUFSIZ - 1, f ); n = atoi( buf ); fclose( f ); return n; } //--------------------------------------------------------------------------------------- // считывание названия городов ( вершин ) из заданного текстового файла // в качестве ответа функция вернет массив вершин графа ( с инициализацией ) // name_file - имя входного текстового файла с данными // vertexes_count - количество вершин графа //--------------------------------------------------------------------------------------- Vertex* Read_name_towns_from_text_file( const char* const name_file, const int vertexes_count ) { char buf[ BUFSIZ ]; FILE* f; int i; Vertex* vertexes = NULL; vertexes = ( Vertex* )malloc( sizeof ( Vertex ) * vertexes_count ); f = fopen( name_file, "r" ); fgets( buf, BUFSIZ - 1, f ); for ( i = 0; i < vertexes_count; i++ ) { fgets( buf, BUFSIZ - 1, f ); buf[ strlen( buf ) - 1 ] = 0; vertexes[ i ].name = ( char* )malloc( strlen( buf ) + 1 ); strcpy( vertexes[ i ].name, buf ); vertexes[ i ].distance = INT_MAX; vertexes[ i ].status = UNVISITED; vertexes[ i ].from = -1; } fclose( f ); return vertexes; } //--------------------------------------------------------------------------------------- // удаление вершин графа из памяти // vertexes - массив городов ( вершин графа ) // vertexes_count - количество вершин //--------------------------------------------------------------------------------------- Vertex* Delete_vertexes( Vertex* vertexes, const int vertexes_count ) { int ivertex; for ( ivertex = 0; ivertex < vertexes_count; ivertex++ ) { free( vertexes[ ivertex ].name ); } free( vertexes ); vertexes = NULL; return vertexes; } //--------------------------------------------------------------------------------------- // удаление из памяти весовой матрицы графа // matrix - весовая матрица // vertexes_count - количество вершин графа //--------------------------------------------------------------------------------------- int** Delete_matrix( int** matrix, const int vertexes_count ) { int ivertex; for ( ivertex = 0; ivertex < vertexes_count; ivertex++ ) { free( matrix[ ivertex ] ); } free( matrix ); matrix = NULL; return matrix; } //--------------------------------------------------------------------------------------- // получение индекса вершины по ее названию - вспомогательная функция // vertexes - одномерный массив городов ( вершин графа ) // vertexes_count - количество городов ( вершин ) // name_town - название города ( метка вершины ) //--------------------------------------------------------------------------------------- int Get_index_vertex_by_name_town( const Vertex* const vertexes, const int vertexes_count, const char* const name_town ) { int ivertex; int index = -1; for ( ivertex = 0; ivertex < vertexes_count; ivertex++ ) { if ( strcmp( vertexes[ ivertex ].name, name_town ) == 0 ) { index = ivertex; break; } } return index; } //--------------------------------------------------------------------------------------- // чтение из текстового файла стоимость проездов между городами // в качестве ответа возвращается весовая матрица графа // vertexes - одномерный массив городов ( вершин графа ) // vertexes_count - количество городов ( вершин ) // name_file - имя входного текстового файла с данными //--------------------------------------------------------------------------------------- int** Read_weight_from_text_file( const Vertex* const vertexes, const int vertexes_count, const char* const name_file ) { FILE* f; int** matrix = NULL; int i; char buf[ BUFSIZ ]; char town_from[ BUFSIZ ]; int index_town_from; char town_to[ BUFSIZ ]; int index_town_to; int weight; matrix = ( int** )malloc( sizeof( int* ) * vertexes_count ); for ( i = 0; i < vertexes_count; i++ ) { matrix[ i ] = ( int* )calloc( vertexes_count, sizeof( int ) ); } f = fopen( name_file, "r" ); for ( i = 0; i < vertexes_count + 2; i++ ) { fgets( buf, BUFSIZ - 1, f ); } while ( 1 ) { fgets( buf, BUFSIZ - 1, f ); if ( buf[ strlen( buf ) - 1 ] == '\n' ) { buf[ strlen( buf ) - 1 ] = 0; } sscanf( buf, "%s - %s %d", town_from, town_to, &weight ); index_town_from = Get_index_vertex_by_name_town( vertexes, vertexes_count, town_from ); index_town_to = Get_index_vertex_by_name_town( vertexes, vertexes_count, town_to ); matrix[ index_town_from ][ index_town_to ] = matrix[ index_town_to ][ index_town_from ] = weight; if ( feof( f ) ) { break; } } fclose( f ); return matrix; } //--------------------------------------------------------------------------------------- // среди всех вершин, имеющих статус "В работе" отбирается та, у которой минимальная ценовая метка пути // vertexes - одномерный массив городов ( вершин графа ) // vertexes_count - количество городов ( вершин ) //--------------------------------------------------------------------------------------- int Get_index_next_work_vertex( const Vertex* const vertexes, const int vertexes_count ) { int ivertex; int index = -1; int distance_min = INT_MAX; for ( ivertex = 0; ivertex < vertexes_count; ivertex++ ) { if ( ( vertexes[ ivertex ].status == WORK ) and ( vertexes[ ivertex ].distance < distance_min ) ) { index = ivertex; distance_min = vertexes[ ivertex ].distance; } } return index; } //--------------------------------------------------------------------------------------- // Алгоритм Дейкстры. Находим кратчайшие пути от вершины с индексом index_start до всех остальных // vertexes - одномерный массив городов ( вершин графа ) // vertexes_count - количество городов ( вершин ) // matrix - отвечает за стоимость проезда по дорогам ( весовая матрица графа ) // index_start - индекс вершины, от которой запускается Дейкстра //--------------------------------------------------------------------------------------- void Dijkstra( Vertex* const vertexes, const int vertexes_count, const int** const matrix, const int index_start ) { int index; int j; vertexes[ index_start ].distance = 0; vertexes[ index_start ].status = WORK; vertexes[ index_start ].from = -1; while ( 1 ) { // находим индекс вершины с минимальной ценовой меткой index = Get_index_next_work_vertex( vertexes, vertexes_count ); // если все вершины графа обработаны, то алгоритм завершается if ( index == -1 ) { break; } // перебираем всех соседей текущей вершины ( у этой вершины наименьшая цена проезда ) for ( j = 0; j < vertexes_count; j++ ) { if ( index == j ) { continue; } // если расстояние до соседней вершины меньше, чем текущее, то пересчитываем это расстояние if ( ( matrix[ index ][ j ] > 0 ) and ( vertexes[ j ].status != VISITED ) and ( vertexes[ index ].distance + matrix[ index ][ j ] < vertexes[ j ].distance ) ) { vertexes[ j ].from = index; vertexes[ j ].status = WORK; vertexes[ j ].distance = vertexes[ index ].distance + matrix[ index ][ j ]; } } // после перебора всех соседей и релаксации текущая вершина становится посещенной и // в дальнейших вычислениях участия больше не принимает vertexes[ index ].status = VISITED; } } //--------------------------------------------------------------------------------------- // рекурсивный вывод кратчайшего пути между заданными городами ( перечислением городов ) // vertexes - одномерный массив городов ( вершин графа ) // index - индекс обрабатываемой вершины // index_goal - индекс конечной вершины выводимого пути //--------------------------------------------------------------------------------------- void Print_path( const Vertex* const vertexes, const int index, const int index_goal ) { if ( vertexes[ index ].from == -1 ) { printf( "\'%s\' - ", vertexes[ index ].name ); return; } Print_path( vertexes, vertexes[ index ].from, index_goal ); printf( "\'%s\'", vertexes[ index ].name ); if ( index != index_goal ) { printf( " - " ); } } //--------------------------------------------------------------------------------------- // главная функция программы ( точка входа ) //--------------------------------------------------------------------------------------- int main( void ) { #define START 0 // индекс вершины, от которой ищутся кратчайшие пути до всех остальных вершин #define FINISH 4 // индекс вершины, до которой интересует кратчайший путь #define NAME_FILE "input.txt" // имя входного текстового файла с данными // массив городов ( вершин графа ) и их количество, а также весовая целочисленная матрица Vertex* vertexes = NULL; int vertexes_count; int** matrix = NULL; // русификация диалогов программы setlocale( LC_ALL, "Russian" ); // последовательно считываем из заданного текстового файла // количество городов ( вершин ) // названия городов ( меток ) // стоимость проезда по дорогам, связывающих города ( веса ребер ) vertexes_count = Get_vertexes_count_from_text_file( NAME_FILE ); vertexes = Read_name_towns_from_text_file( NAME_FILE, vertexes_count ); matrix = Read_weight_from_text_file( vertexes, vertexes_count, NAME_FILE ); // запускаем алгоритм Дейкстры от вершины с индексом START Dijkstra( vertexes, vertexes_count, matrix, START ); // выводим "расстояние" кратчайшего пути между двумя заданнами городами ( между START и FINISH ) printf( "Кратчайший путь между \'%s\' и \'%s\' = %d ед.\n", vertexes[ START ].name, vertexes[ FINISH ].name, vertexes[ FINISH ].distance ); // построение пути, перечисляя названия городов printf( "Маршрут имеет вид: \n\t" ); Print_path( vertexes, FINISH, FINISH ); // удаляем память из-под массива вершин графа и матрицы весов vertexes = Delete_vertexes( vertexes, vertexes_count ); matrix = Delete_matrix( matrix, vertexes_count ); // легкая проверка на утечки памяти printf( "\n\nУтечки памяти ( 0 - НЕТ; 1 - ДА ): %d\n\n", _CrtDumpMemoryLeaks() ); // задержка программы, чтобы у пользователя была возможность просмотреть результаты system( "pause" ); return EXIT_SUCCESS; } //--------------------------------------------------------------------------------------- |
➡ Программа под $350$ строк кода. А на языке Си так всегда — не бывает коротких программ, так как каждый чих нужно программировать, в отличие, например, от языка С++, где есть куча готовых шаблонов.
Напомню, что алгоритм Дейкстры я накладываю на следующий граф:

Рисунок — схема дорог, связывающих города
Тестирую программу для нахождения кратчайшего пути между Москвой и Новгородом:
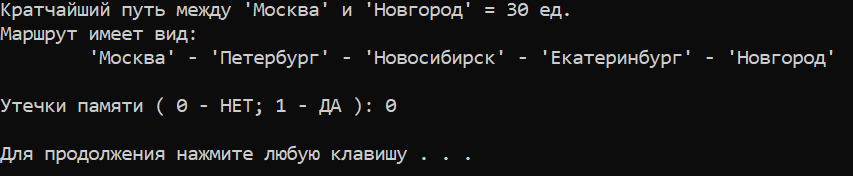
Рисунок — результаты работы программы ( поиск минимального пути между Москвой и Новгородом )
А что будет, если какая-то вершина графа недостижима от заданной
Да, не всегда можно проложить путь до каждой вершины графа. Если граф имеет более одной компоненты связности, то некоторые вершины физически будут недостижимы.
Что в этом случае вернет представленная программа в качестве ответа?
Ответить просто на этот вопрос, если помнить инициализацию вершин графа перед началом запуска алгоритма Дейкстры. Всем вершинам присваивалась ценовая метка, равная «плюс бесконечности»:
|
1 |
vertexes[ i ].distance = INT_MAX; |
Следовательно, если после выполнения алгоритмы Дейкстры минимальное расстояние до какой-либо вершины равное $\infty$, значит, проехать до этой вершины физически невозможно!
Хочу это проверить на практике. Добавлю $8$-ой город, например, Челябинск. Это будет изолированная вершина графа. И попробую найти самый дешевый путь от Петербурга до Челябинска.
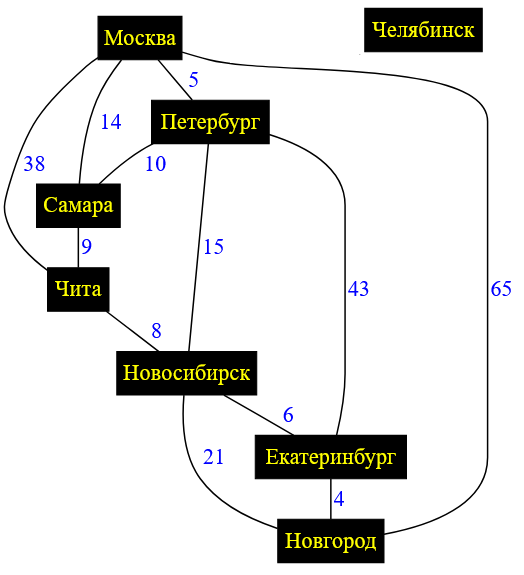
Рисунок — в схему дорог добавлен город Челябинск, который не связан ни с одним городом
Автоматически совсем чуть-чуть меняется и входной текстовый файл с информацией о городах и связях между ними:
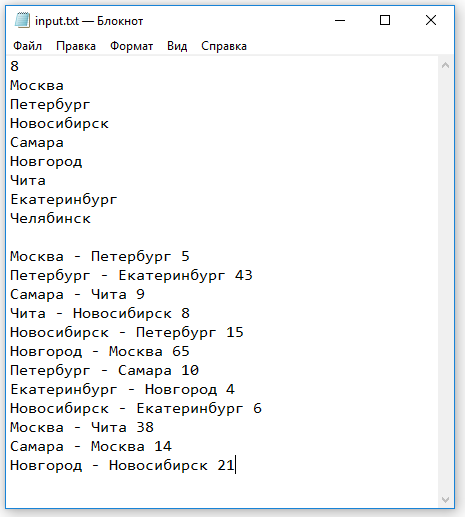
Рисунок — входной текстовый файл теперь содержит информацию о Челябинске
В результате программа выдает следующие результаты:
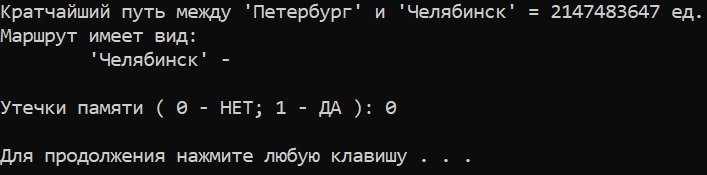
Рисунок — результаты, когда кратчайший путь невозможно проложить
Понятно, что можно вывести на экран соответствующее информативное сообщение, но я писал программу отталкиваясь от факта, что граф явялется связным, то есть есть маршрут из любой вершины в любую другую. Оставляю вам самостоятельно сделать эту элементарную доработку.
Добавить комментарий