| ВНИМАНИЕ |
Для заказа программы на графы и графовые алгоритмы пишите на мой электронный адрес proglabs@mail.ru |
В этой статье-шпаргалке покажу алгоритм нахождения степеней вершин в неориентированном невзвешенном графе.
Например, есть такой помеченный граф, состоящий из $9$ вершин:
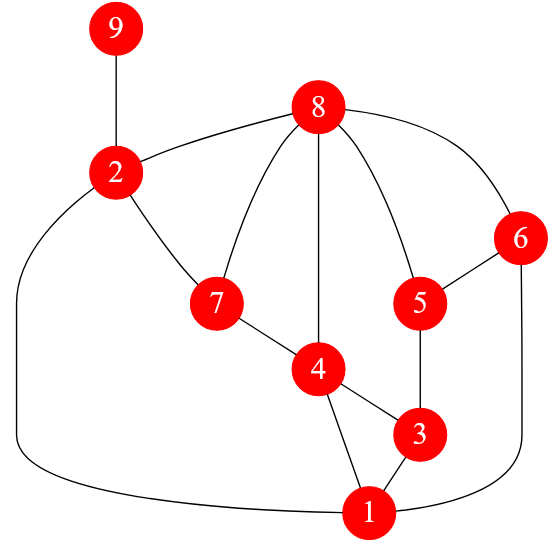
Рисунок — неориентированный невзвешенный граф, состоящий из $9$ вершин
Степенью вершины неориентированного графа называется количество ребер, инцидентных этой вершине.
Другими словами, надо подсчитать количество ребер, входящих/выходящих для каждой вершины заданного графа.
Хочу посмотреть на вершину $5$ и рассчитать ее степень. Для этого нужно отобрать все ребра, инцидентные этой вершине:
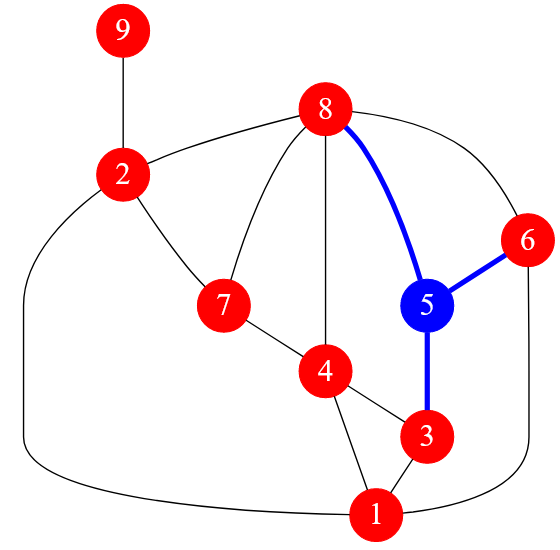
Рисунок — вычисление степени $5$-ой вершины
➡ Из рисунка видно, что $5$-ой вершине инциденты только $3$ ребра. Следовательно, степень вершины с меткой $5$ равна $3$.
На всех последующих изображениях степени вершин будут показаны рядом с вершиной синим цветом шрифта.
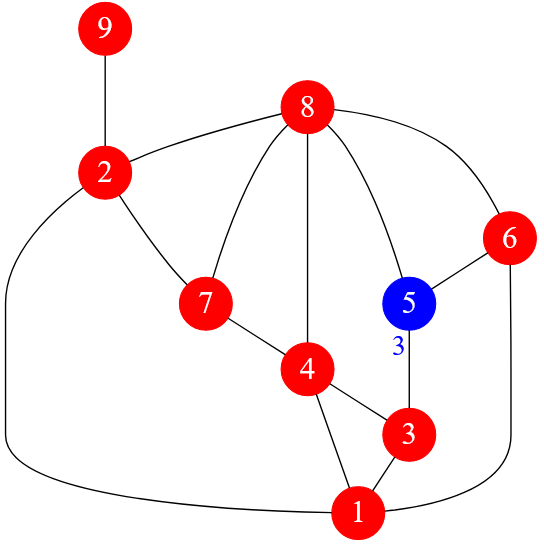
Рисунок — степень $5$-ой вершины равна $3$
Теперь я проставлю степени для каждой вершины графа:
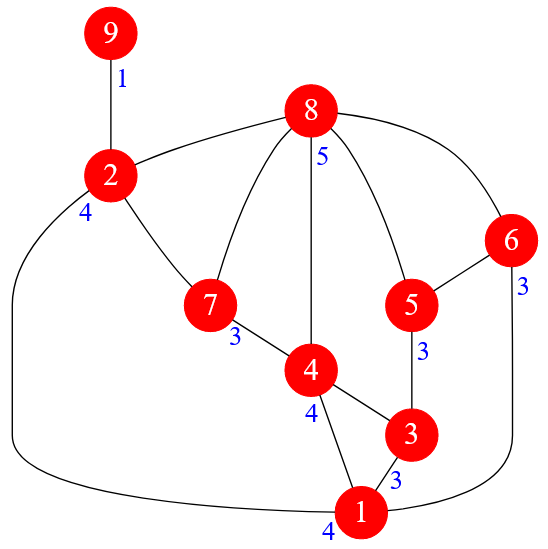
Рисунок — вершины графа с их степенями
Самая частая степень — это $3$. Одна вершина ( с меткой $9$ ) имеет степень, равную $1$, а еще одна ( с меткой $8$ ) — $5$.
💡 Есть такая очевидная зависимость между количеством ребер неориентированного графа и суммой степеней всех его вершин:
сумма степеней вершин графа равна удвоенному числу его ребер.
Общее количество ребер исходного графа — $15$ шт.
Сумма степеней всех вершин, начиная с первой по порядку: $4\ +\ 4\ +\ 3\ +\ 4\ +\ 3\ +\ 3\ +\ 3\ +\ 5\ +\ 1\ =\ 30$
➡ $30\ =\ $$2$$\ \cdot 15$ — истина!
Все расчеты, приведенные выше, были выполнены визуально. Поэтому я ставлю такой вопрос:
Как программно определить степень каждой вершины заданного неориентированного графа?
Для этого нужно заданный граф отобразить в структуры данных. Я воспользуюсь классической матрицей смежности ( квадратная матрица порядка $n$ ( $n$ — количество вершин ), состоящая из $0$ и $1$ ).
| $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | |
| $1$ | $0$ | $1$ | $1$ | $1$ | $0$ | $1$ | $0$ | $0$ | $0$ |
| $2$ | $1$ | $0$ | $0$ | $0$ | $0$ | $0$ | $1$ | $1$ | $1$ |
| $3$ | $1$ | $0$ | $0$ | $1$ | $1$ | $0$ | $0$ | $0$ | $0$ |
| $4$ | $1$ | $0$ | $1$ | $0$ | $0$ | $0$ | $1$ | $1$ | $0$ |
| $5$ | $0$ | $0$ | $1$ | $0$ | $0$ | $1$ | $0$ | $1$ | $0$ |
| $6$ | $1$ | $0$ | $0$ | $0$ | $1$ | $0$ | $0$ | $1$ | $0$ |
| $7$ | $0$ | $1$ | $0$ | $1$ | $0$ | $0$ | $0$ | $1$ | $0$ |
| $8$ | $0$ | $1$ | $0$ | $1$ | $1$ | $1$ | $1$ | $0$ | $0$ |
| $9$ | $0$ | $1$ | $0$ | $0$ | $0$ | $0$ | $0$ | $0$ | $0$ |
Степенью $i$-ой вершины будет сумма всех единиц $i$-ой строки ( или колонки ) этой матрицы смежности. Закодировать этот тривиальный алгоритм, разумеется, элементарно.
➡ Вот пример программы на языке Си, которая на вход принимает неориентированный граф в формате матрицы смежности, а в качестве ответа выпечатывает на экран степень каждой вершины графа.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 |
#include <stdio.h> #include <stdlib.h> #include <locale.h> // количество вершин графа #define VERTEX_COUNT 9 //--------------------------------------------------------------------- // вычисление степени заданной ( по индексу ) вершины графа //--------------------------------------------------------------------- int Get_degree_vertex( const int matrix[][ VERTEX_COUNT ], const int index_vertex ) { int index; int degree = 0; for ( index = 0; index < VERTEX_COUNT; index++ ) { degree += matrix[ index_vertex ][ index ]; } return degree; } //--------------------------------------------------------------------- // вычисление степеней всех вершин заданного графа //--------------------------------------------------------------------- void Get_degree_vertexes( const int matrix[][ VERTEX_COUNT ], int degrees[] ) { int index_vertex; for ( index_vertex = 0; index_vertex < VERTEX_COUNT; index_vertex++ ) { degrees[ index_vertex ] = Get_degree_vertex( matrix, index_vertex ); } } //--------------------------------------------------------------------- // вывод степеней вершин графа на экран //--------------------------------------------------------------------- void Print_degrees( const int degrees[] ) { int index_vertex; printf( "Степени вершин заданного неориентированного графа:\n" ); for ( index_vertex = 0; index_vertex < VERTEX_COUNT; index_vertex++ ) { printf( "\t- вершина #%d имеет степень, равную %d\n", index_vertex + 1, degrees[ index_vertex ] ); } } //--------------------------------------------------------------------- // главная функция программы ( точка входа ) //--------------------------------------------------------------------- int main( void ) { // фиксированная матрица смежности неориентированного графа, // рассмотренного в статье на сайте const int matrix[ VERTEX_COUNT ][ VERTEX_COUNT ] = { 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0 }; // массив хранит степени соответсвенных вершин int degrees[ VERTEX_COUNT ] = { 0 }; // русификация диалогов программы setlocale( LC_ALL, "Russian" ); // вычисление степеней вершин и вывод результата на экран Get_degree_vertexes( matrix, degrees ); Print_degrees( degrees ); // задержка работы программы, чтобы у пользователя была возможность просмотреть результат printf( "\n\n" ); system( "pause" ); return EXIT_SUCCESS; } |
Результаты работы программы:
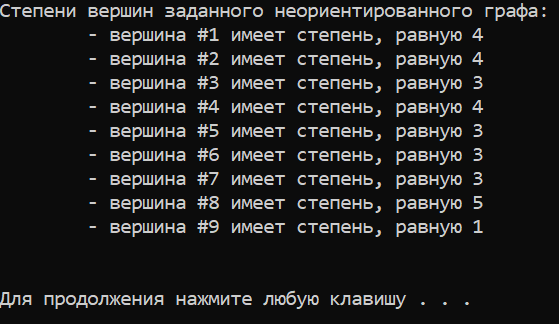
Рисунок — результаты работы программы
Какова сложность алгоритма нахождения степеней вершин в неориентированном графе?
Чтобы посчитать степень одной ( любой ) вершины, нужно просмотреть всю строку в матрице смежности. Эта строка, по сути, одномерный массив, состоящий из $0$ и $1$ длины $n$, где $n$ — количество вершин графа. То есть сложность алгоритма определения степени конкретной вершины графа составляет $O$$( n )$, а поскольку требуется понять сложность определения всех вершин графа, которых $n$ штук, то общая алгоритмическая сложность будет квадратичной, то есть $O$$( n^2 )$.
💡 Информация о степенях вершин графа находит применение в других графовых алгоритмах.
Например, если нужно найти гамильтонов цикл в заданном графе, то предварительно нужно доказать, что граф является гамильтоновым. Для этого стоит воспользоваться условием Оре или Поша. А эти алгоритмы ( условия ) оперируют степенями вершин.
➡ Пишите в комментариях, что непонятно в алгоритме определения степеней вершин неориентированного графа, а также в каких алгоритмах вам пригодилась эта «степенная» информация.
Материал подготовил Александр Георгиевич, специалист по динамическим структурам данных и графовым алгоритмам: стеки, деки, списки, деревья, хеш-таблицы, графы и т.п. Для записи на частную подготовку или заказа работы по программированию звонить по номеру телефона: 8(926) 610 — 61 — 95 (электронный адрес: proglabs@mail.ru).
Добавить комментарий