| ВНИМАНИЕ |
Для заказа программы на графовые алгоритмы любой сложности пишите на мой электронный адрес proglabs@mail.ru |
Перед тем, как приступить к исследованию алгоритма обхода графа в ширину, сразу договоримся, что все графы, которые будут представлены в этой статье, являются связными.
Неориентированный граф называется связным, если любую его вершину можно достигнуть из любой другой вершины.
➡ Граф также является связным, если он состоит из одной компоненты связности.
➡ Взвешенность графа ни коим образом не влияет на алгоритм обхода в ширину. Поэтому все графы из этого материала будут также невзвешенными.
Хочу рассмотреть следующий помеченный связный неориентированный невзвешенный граф:
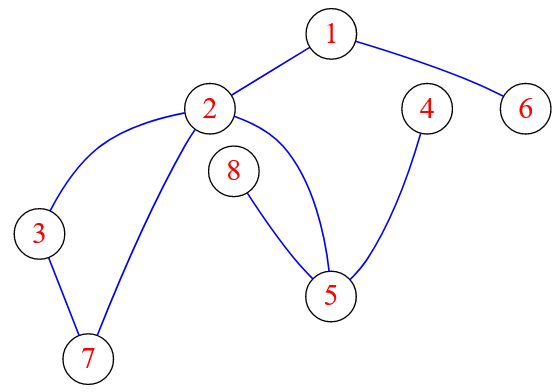
Рисунок — неориентированный связный граф, состоящий из $8$ вершин
Моя задача, используя алгоритм DFS, обойти все вершины этого графа.
Для начала я определюсь с вершиной, от которой будет запущен алгоритм поиска в глубину. По-большему счету, это непринципиально, но, например, я выберу вершину с меткой $3$:
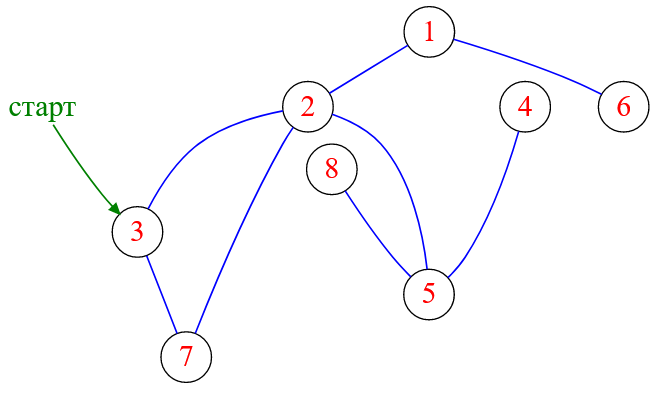
Рисунок — алгоритм обхода графа в глубину начинается от вершины с меткой $3$
Также мне потребуется отличать статус вершин в процессе работы алгоритма. Каждая вершина графа может принимать один из трех статусов ( статусы буду обозначать через цвет вершины ):
| Цвет вершины | Статус вершины |
| Вершина еще не посещена. | |
| Вершина посещена ( находится в работе ), но обработаны еще не все исходящие из нее ребра. | |
| Вершина обработана и все ребра, исходящие из нее, также обработаны. |
➡ Очевидно, что до начала работы алгоритма все вершины графа имеют белый цвет, то есть непосещены.
Поиск в ширину стартует с вершины, имеющей метку $3$, поэтому изменим статус этой вершины на «в работе»:
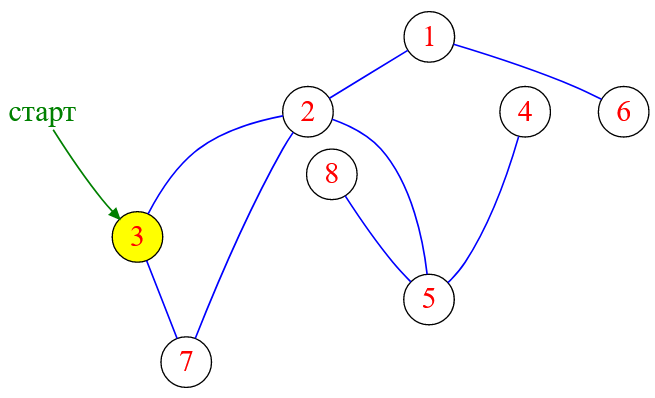
Рисунок — DFS запускается от вершины с меткой $3$
Затем нужно попробовать найти смежную вершину, имеющую статус непосещенной. Для этого следует перебрать все ребра, инцидентные текущей вершине. В моем случае, это вершина с меткой $3$. По-большему счету непринципиально, в какой последовательности искать непосещенную смежную вершину, но я буду перебирать по возрастанию числовых меток.
Вершина с меткой $3$ имеет двух соседей: это вершины с метками $2$ и $7$. Причем оба «соседа» имеют статус непосещенных. Я выбираю вершину с меткой $2$ и меняю ее статус на «в работе».
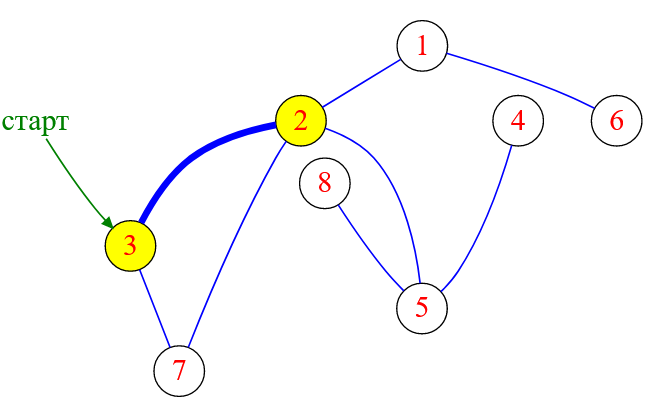
Рисунок — алгоритм DFS «перекидывается» на вершину с меткой $2$
➡ На данный момент «в работе» две вершины ( их метки $2$ и $3$ ), но текущей вершиной выступает вершина с меткой $2$.
Сейчас для вершины с меткой $2$ повторяем те же действия, что и для вершины с меткой $3$ — находим «белого» соседа с минимальной меткой. Это вершина с меткой $1$.
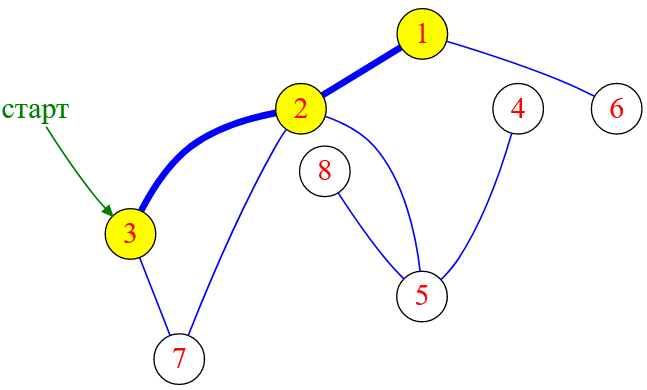
Рисунок — алгоритм DFS «перекидывается» на вершину с меткой $1$
От вершины с меткой $1$ DFS продолжает свое движение к вершине с меткой $6$.
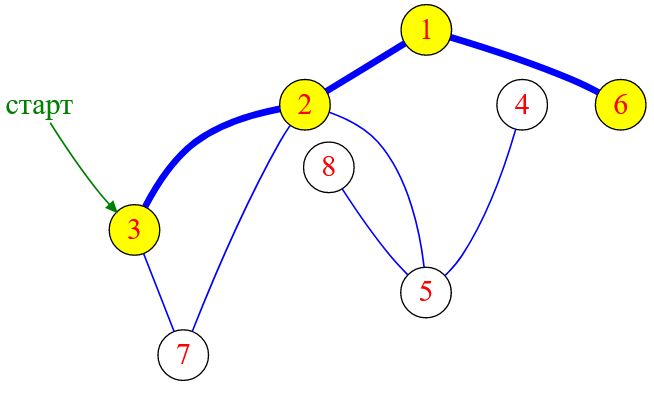
Рисунок — алгоритм DFS «перекидывается» на вершину с меткой $6$
И вот мы добрались до так называемого тупика!
Вершина называется тупиковой, если она не содержит исходящих ребер, ведущих в непосещенные вершины.
Вершина с меткой $6$ является именно тупиковой. Она имеет одно ребро, которое ведет в уже посещенную вершину, то есть в вершину графа с меткой $1$.
➡ Если обход графа добрался до тупиковой вершины, то необходимо возвращаться вдоль пройденного пути, пока не найдется вершина, имеющая исходящие ребра, ведущие в еще непосещенные вершины, и из этой вершины DFS продолжает свое движение по одному из таких ребер.
➡ Не стоит забывать, как только все исходящие ребра текущей вершины рассмотрены, то и сама вершина считается обработанной. Следовательно, эта вершина становится черной.
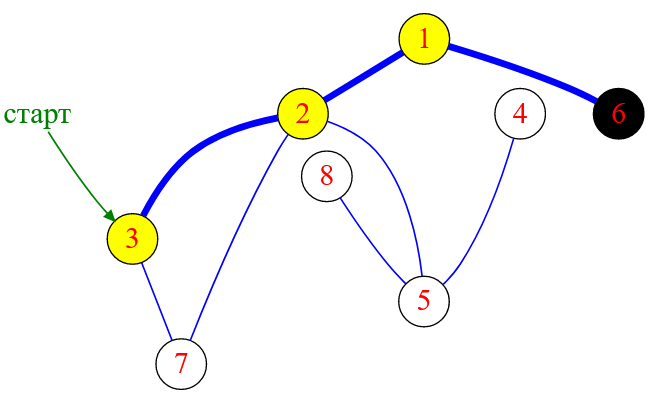
Рисунок — вершина графа с меткой $6$ считается обработанной и в дальнейших вычислениях участия не принимает
Алгоритм поиска в глубину возвращается к вершине с меткой $1$, но эта вершина не имеет необработанных исходящих ребер. Следовательно, это вершина становится черной ( обработанной ).
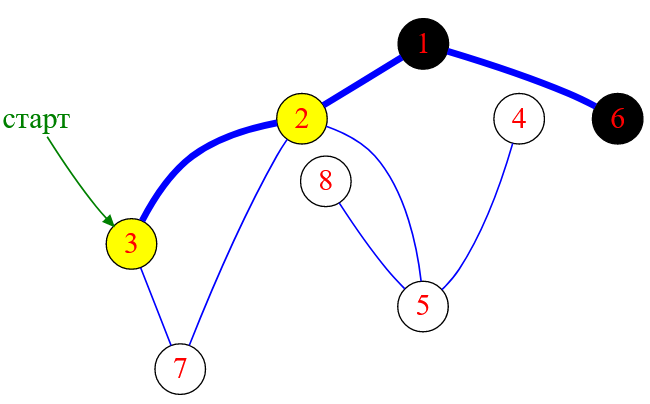
Рисунок — вершина графа с меткой $1$ считается обработанной и в дальнейших вычислениях участия не принимает
Вершина с меткой $2$ имеет четыре исходящих ребра. Ребра, ведущие к вершинам $1$ и $3$, уже обработаны, поэтому выбирать надо из ребер, ведущих к вершинам с меткой $5$ или $7$. Так как я перебираю ребра по возрастанию числовых меток, то моя реализация алгоритма обхода в глубину выберет движение к вершине с меткой $5$.
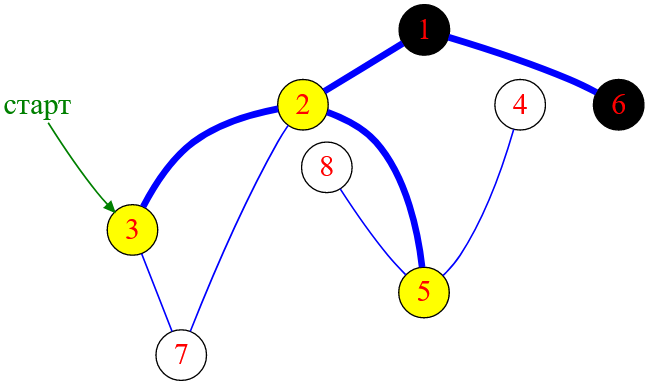
Рисунок — алгоритм DFS «перекидывается» на вершину с меткой $5$
От вершины с меткой $5$ алгоритм DFS выберет движение к еще непосещенной вершине с минимальной числовой меткой, то есть к узлу с меткой $4$.
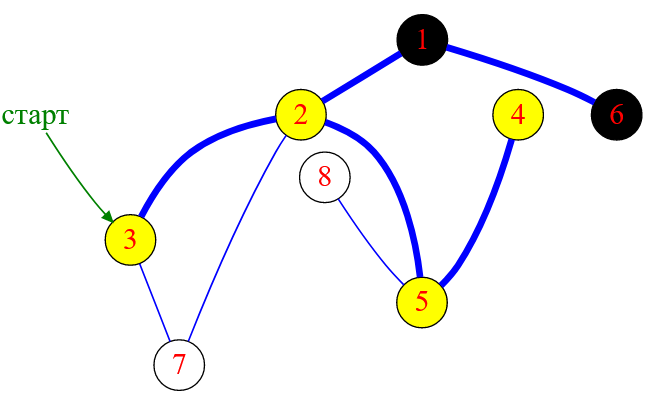
Рисунок — алгоритм DFS «перекидывается» на вершину с меткой $4$
Узел графа с меткой $4$ является тупиковым, поэтому обход в глубину начнет обратное движение и перейдет к вершине с меткой $8$.
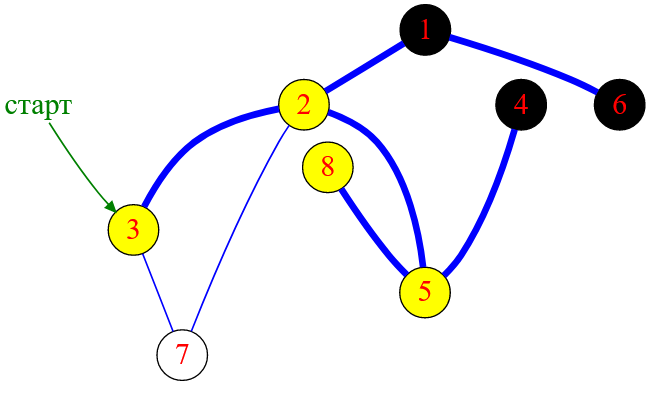
Рисунок — алгоритм DFS «перекидывается» на вершину с меткой $8$
Теперь вершина с меткой $8$ стала тупиковой и DFS возвращается к предшествующей вершине, то есть к вершине с меткой $5$. Этот узел также является тупиковым, поэтому алгоритм делает еще один шаг назад и возвращается к узлу с меткой $2$. После этого алгоритм уходит к еще непосещенной вершине с меткой $7$.
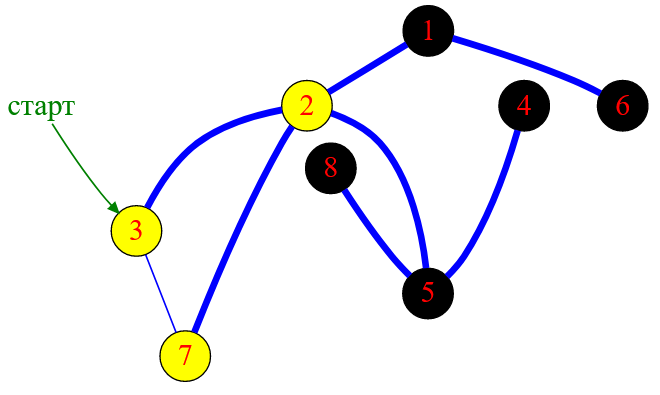
Рисунок — алгоритм DFS «перекидывается» на вершину с меткой $7$
Вершины с метками $7$ и $2$ являются обработанными и, в итоге, алгоритм обхода графа в глубину подошел к финишу.
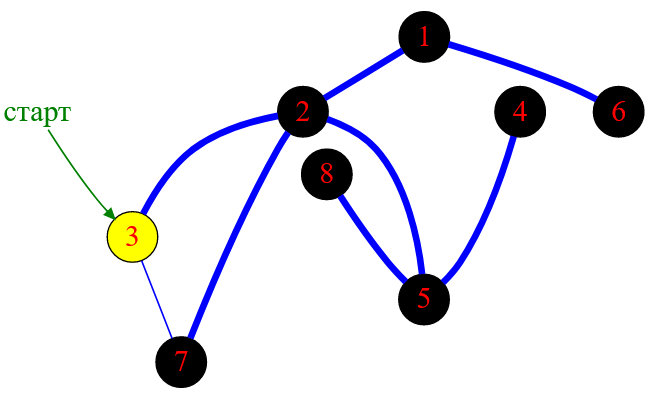
Рисунок — предпоследний этап алгоритма обхода графа в глубину ( DFS )
На завершающем этапе проверяется стартовая вершина с меткой $3$. Все ее исходящие ребра обработаны, поэтому она принимает статус обработанной ( закрашивается в черный цвет ), и алгоритм поиска в глубину заканчивается.
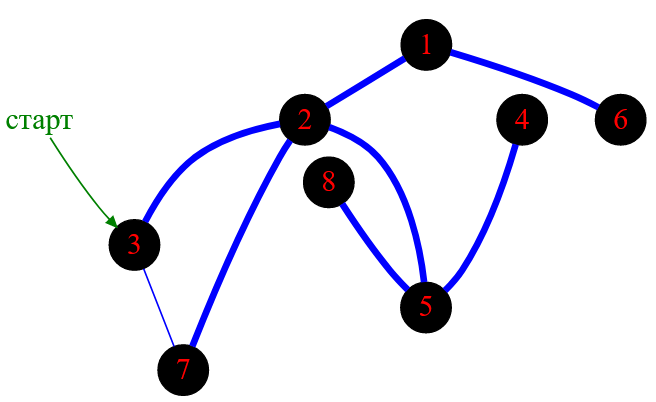
Рисунок — состояние графа после обхода его в глубину ( DFS )
➡ Все вершины графа имеют черный цвет. Это означает, что они были посещены, а также все исходящие ребра каждой вершины были проверены.
➡ Также стоит запомнить, что алгоритм DFS заканчивает свою обработку на той вершине, с которой начинался. В моем примере эта вершина с меткой $3$.
В процессе работы алгоритма строится так называемое дерево поиска в глубину. Это дерево показывает зависимость между вершинами в порядке их обхода.
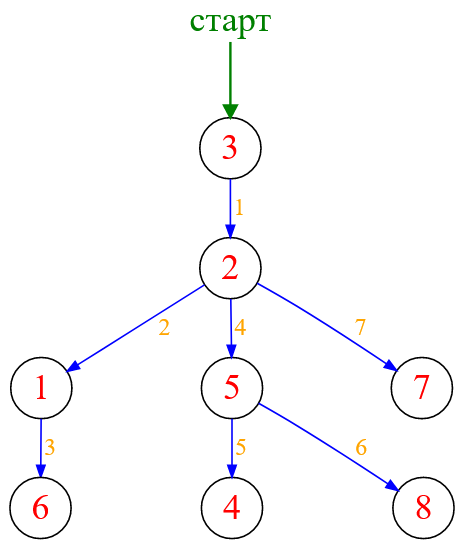
Рисунок — дерево поиска в глубину
➡ Оранжевые числа показывают номер шага, на котором была посещена вершина графа. Это дерево крайне удобно и полезно для анализа результатов алгоритма DFS.
Например, из представленного дерева видно, что вершина с меткой $6$ была посещена на $3$-ем шаге работы алгоритма.
➡ Также благодаря этому дереву можно проследить маршрут достижения той или иной вершины от стартовой. Например, для вершины с меткой $7$ маршрут будет таким: $7$ — $2$ — $3$.
Но подобные маршруты не являются кратчайшими с точки зрения достижения заданной вершины от стартовой.
Всю эту сопутствующую информацию я распечатаю в своей программе, которая идет ниже в данной статье.
Касательно оценки сложности, представленного алгоритма обхода неориентированного графа в глубину, заданного матрицей смежности.
Рекурсивная функция DFS будет вызвана по одному разу для каждой вершины заданного графа ( напомню, что на рассмотрении был граф, состоящий из $8$ вершин ). В рамках этой функции требуется находить все инцидентные этой вершине ребра. Для этого придется просматривать полностью всю строку с информацией из матрицы смежности. Матрица смежности — квадратная матрица порядка $n$, где $n$ — количество вершин графа.
Получается, что нужно $n$ раз просмотреть $n$ ячеек из матрицы смежности. Следовательно, сложность данного алгоритма $O( n^2 )$. Еще говорят, что алгоритм обладает квадратичной сложностью.
💡 Для сильно связных графов, стремящихся к полным, представление их структуры в формате матрицы смежности вполне оправданно. Но если граф является разреженным, то удобнее применять список смежности.
В результате я написал программу на языке «чистый» Си ( стандарт C89-90 ), в которой реализован рассмотренный алгоритм обхода графа в глубину, заданного матрицей смежности.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 |
#include <stdio.h> #include <stdlib.h> #include <locale.h> // статусы вершин графа typedef enum Status { WHITE, // непосещена YELLOW, // посещена ( находится в работе ) BLACK // обработана ( не находится в работе ) } Status; // описание сущности "Вершина графа" typedef struct Vertex { Status status; int parent; } Vertex; // количество вершин заданного помеченного связного неориентированного невзвешенного графа ( взят пример из статьи на сайте ) #define VERTEXES_COUNT 8 // прототипы пользовательских функций void Init_vertexes( Vertex [] ); void DFS( Vertex [], const int [][ VERTEXES_COUNT ], const int ); void Print_child_parent_vertex( const Vertex[] ); void Print_path( const Vertex[], int ); //------------------------------------------------------------------------------------------------------- // главная функция программы ( точка входа ) //------------------------------------------------------------------------------------------------------- int main( void ) { const int matrix[ VERTEXES_COUNT ][ VERTEXES_COUNT ] = { 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0 }; Vertex vertexes[ VERTEXES_COUNT ]; setlocale( LC_ALL, "Russian" ); Init_vertexes( vertexes ); DFS( vertexes, matrix, 2 ); Print_child_parent_vertex( vertexes ); Print_path( vertexes, 1 ); printf( "\n\n" ); return EXIT_SUCCESS; } //------------------------------------------------------------------------------------------------------- // инициализация информации о вершинах графа //------------------------------------------------------------------------------------------------------- void Init_vertexes( Vertex vertexes[] ) { int i; for ( i = 0; i < VERTEXES_COUNT; i++ ) { vertexes[ i ].status = WHITE; vertexes[ i ].parent = -1; } } //------------------------------------------------------------------------------------------------------- // DFS - обход вершин заданного неориентированного графа в глубину, заданного матрицей смежности //------------------------------------------------------------------------------------------------------- void DFS( Vertex vertexes[], const int matrix[][ VERTEXES_COUNT ], const int current_vertex_index ) { int nearest_vertex_index; vertexes[ current_vertex_index ].status = YELLOW; // цикл по всем ребрам, исходящим из текущей вершины ( ее индекс current_vertex_index ) for ( nearest_vertex_index = 0; nearest_vertex_index < VERTEXES_COUNT; nearest_vertex_index++ ) { if ( ( matrix[ current_vertex_index ][ nearest_vertex_index ] == 1 ) && ( vertexes[ nearest_vertex_index ].status == WHITE ) ) { vertexes[ nearest_vertex_index ].parent = current_vertex_index; DFS( vertexes, matrix, nearest_vertex_index ); } } vertexes[ current_vertex_index ].status = BLACK; } //------------------------------------------------------------------------------------------------------- // демонстрация зависимости посещения вершин графа в формате печати родительской вершины //------------------------------------------------------------------------------------------------------- void Print_child_parent_vertex( const Vertex vertexes[] ) { int ivertex; printf( "\nЗависимость дочерняя-родительская вершины\n" ); printf( "------------------------------------------------\n" ); printf( " Дочерняя вершина Родительская вершина\n" ); printf( "------------------------------------------------\n" ); for ( ivertex = 0; ivertex < VERTEXES_COUNT; ivertex++ ) { printf( "%19d", ivertex + 1 ); if ( vertexes[ ivertex ].parent == -1 ) { printf( "%29s\n", "Начальная вершина обхода" ); } else { printf( "%29d\n", vertexes[ ivertex ].parent + 1 ); } } printf( "------------------------------------------------\n" ); } //------------------------------------------------------------------------------------------------------- // вывод маршрута от заданной вершины до стартовой ( маршрут обхода DFS ) //------------------------------------------------------------------------------------------------------- void Print_path( const Vertex vertexes[], int index_vertex ) { printf( "\n\nМаршрут до вершины с меткой %d: %d", index_vertex, index_vertex ); while ( vertexes[ index_vertex - 1 ].parent != -1 ) { printf( " - %d", vertexes[ index_vertex - 1 ].parent + 1 ); index_vertex = vertexes[ index_vertex - 1 ].parent + 1; } } //------------------------------------------------------------------------------------------------------- |
Тестирование программы проведу на графе из этой статьи. Дополнительно распечатаю маршрут посещения алгоритмом DFS вершины с меткой $8$.
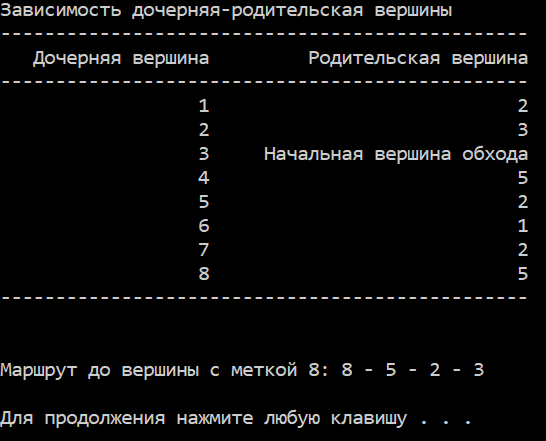
Рисунок — результаты работы программы ( алгоритм DFS )
Обход ( поиск ) графа в глубину нашел широчайшее применение при обработке графов. Вообще, DFS — один из популярнейших алгоритмов предобработки графовых структур в рамках других графовых алгоритмов.
DFS применяют при:
➡ обходе вершин графа;
➡ нахождении количества компонент связности ( проверке графа на связность );
➡ топологической сортировке;
➡ определении мостов;
➡ определении точек сочленения;
➡ нахождении компонент сильной связности.
💡 И это далеко не полный перечень алгоритмов, где без DFS не обойтись.
Пишите в комментариях, что непонятно в рамках рассмотренного алгоритма обхода графа в глубину. Также расскажите, в каких алгоритмах или практических задачах вам пришлось применить DFS.
| ВНИМАНИЕ |
Для заказа программы на графовые алгоритмы любой сложности пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий