| ВНИМАНИЕ | Для заказа программы на двоичное дерево поиска пишите на мой электронный адрес proglabs@mail.ru |
Иногда мне приходится искать количество неполных вершин ( я их также называю половинчатые ) в поисковом двоичном дереве. Решил ( в первую очередь для себя ) написать эту заметку-шпаргалку, чтобы при необходимости быстро вспомнить алгоритм.
Хочу рассмотреть следующее анонимное двоичное дерево поиска:

Рисунок — стандартное анонимное бинарное дерево поиска
➡ Очевидно, чтобы найти количество неполных узлов в бинарном дереве, необходимо знать определения термина «неполный узел», чтобы понимать, а что, собственно, ищем-то.
Неполный узел — узел поискового двоичного дерева, который имеет либо левого, либо правого потомка ( но не оба одновременно ).
Тогда я отмечу все неполные узлы на рассматриваемом анонимном дереве синим цветом:
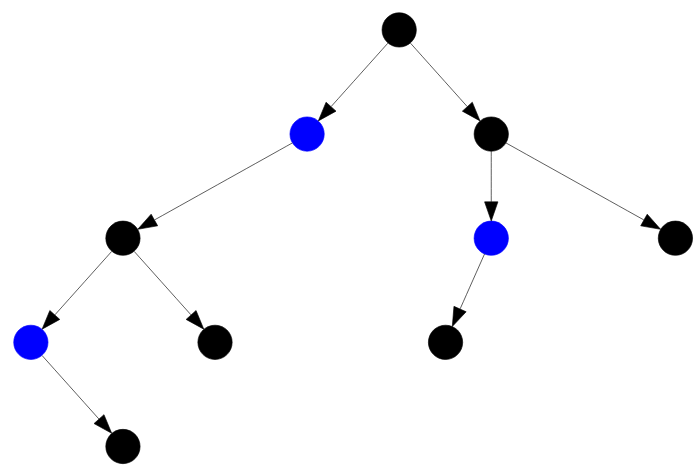
Рисунок — неполные узлы бинарного дерева поиска
Моя задача — понять, каким образом найти все эти «синие» вершины, являющиеся неполными узлами. То есть мне нужна функция, которая в качестве результата вернет количество таких вершин в заданном бинарном поисковом дереве.
Хочу внимательно рассмотреть это анонимное поисковое двоичное дерево, на котором будут отображены все вершинные связи:
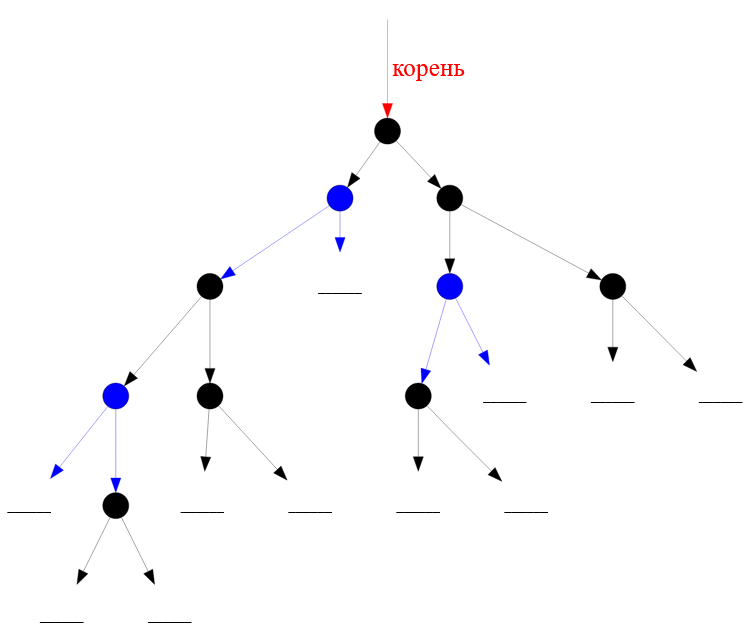
Рисунок — бинарное дерево поиска со всеми связями его вершин
Из рисунка видно, что неполные узлы в отличие от листовых узлов не заканчивают ветвление дерева, следовательно, рекурсивная функция не должна останавливаться, когда встретит на своем пути неполный узел.
➡ Другими словами, один неполный узел может быть родителем по отношению к одному или нескольким неполным узлам.
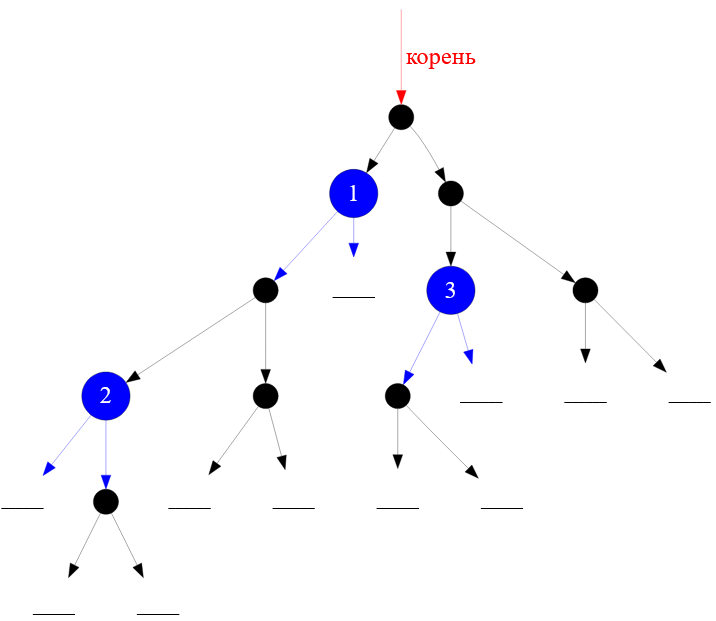
Рисунок — неполный узел $1$ является предком для другого неполного узла $2$
В результате я запрограммировал следующую программную рекурсивную функцию, которая на вход принимает указатель на корень бинарного дерева поиска и в результате возвращает количество неполных вершин, которое оно содержит:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//------------------------------------------------------------------------------ // статус узла бинарного дерева поиска //------------------------------------------------------------------------------ typedef enum Node_status { NONE, // нет узла ( NULL-указатель ) LEAF, // пустой узел ( лист - не имеет сыновей ) HALF, // половинчатый ( имеет одного сына: левого или правого ) FULL // полный ( имеет обоих сыновей ) } Node_status; //------------------------------------------------------------------------------ // нахождение количества неполных ( половинчатых ) вершин в двоичном дереве //------------------------------------------------------------------------------ int Get_half_count( const Node* const node ) { Node_status status = Get_status_node( node ); int is_half = 0; if ( status == NONE ) { return 0; } if ( status == HALF ) { is_half = 1; } return is_half + Get_half_count( node -> left ) + Get_half_count( node -> right ); } //------------------------------------------------------------------------------ |
Функция Get_status_node() принимает указатель на заданную вершину и в качестве ответа возвращает статус этой вершины. Статус может принимать одно из четырех значений, которые определены в перечислении Node_status:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
//------------------------------------------------------------------------------ // определение статуса заданного узла ( лист, половинчатый или полный ) // root - указатель на проверяемый узел ( не должен быть нулевым ) // в качестве ответа возвращается статус проверяемого узла дерева //------------------------------------------------------------------------------ Node_status Get_status_node( const Node* const root ) { // по умолчанию принимаем, что проверяемый узел является половинчатым Node_status status = HALF; // проверка на NULL if ( root == NULL ) { status = NONE; } else { // проверка на лист ( нет ни одного сына ) if ( ( root -> left == NULL ) and ( root -> right == NULL ) ) { status = LEAF; } else { // проверка на полный узел ( имеет обоих сыновей ) if ( ( root -> left != NULL ) and ( root -> right != NULL ) ) { status = FULL; } } } return status; } //------------------------------------------------------------------------------ |
➡ В комментариях пишите, что непонятно по алгоритму нахождения количества неполных вершин в двоичном поисковом дереве, а также, насколько часто вам приходилось на практике сталкиваться с этим алгоритмом.
А в следующей статье я хочу написать, как найти количество полных вершин в заданном дереве. Кстати, алгоритм будет сильно схожим с текущим.
| ВНИМАНИЕ | Для заказа программы на бинарное дерево поиска пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий