| ВНИМАНИЕ | Для заказа программы на бинарное дерево поиска пишите на мой электронный адрес proglabs@mail.ru |
Эта статья — в первую очередь заметка-шпаргалка для себя, так как часто у меня студенты заказывают реализацию бинарного дерева поиска. И одной из вспомогательных операций является нахождение количества полных узлов.
Чтобы понять, как реализовать задуманное, хочу посмотреть на следующее анонимное поисковое двоичное дерево:

Рисунок — стандартное анонимное бинарное дерево поиска
Надо познакомиться с таким термином, как «полный узел«.
Полный узел — вершина двоичного дерева поиска, которая имеет и левого сына, и правого сына одновременно.
Отмечу все полные узлы на приведенном анонимном дереве цветом морской волны:
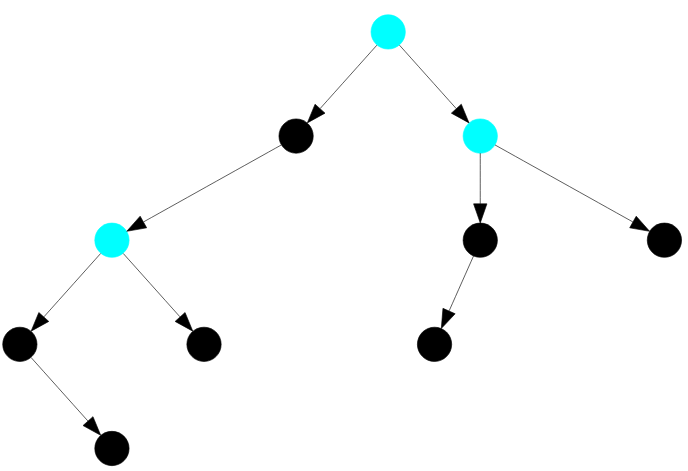
Рисунок — полные узлы бинарного дерева поиска
➡ В предыдущих заметках я показывал, как сосчитать количество листов и неполных узлов в поисковом двоичном дереве. Алгоритм подсчета полных вершин сильно схож с алгоритмом подсчета неполных вершин.
Поэтому сейчас сходу приведу программную реализацию рекурсивной функции на языке Си, которая определяет количество полных узлов в заданном дереве:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
//------------------------------------------------------------------------------ // нахождение количества полных вершин в двоичном дереве поиска //------------------------------------------------------------------------------ int Get_full_count( const Node* const node ) { Node_status status = Get_status_node( node ); int is_full = 0; if ( status == NONE ) { return 0; } if ( status == FULL ) { is_full = 1; } return is_full + Get_full_count( node -> left ) + Get_full_count( node -> right ); } //------------------------------------------------------------------------------ |
Нужно понимать, что некоторые топологии деревьев не имеют ни одной полной вершины. Например, в дереве всего $2$ узла, или двоичное дерево выродилось в линейный список:
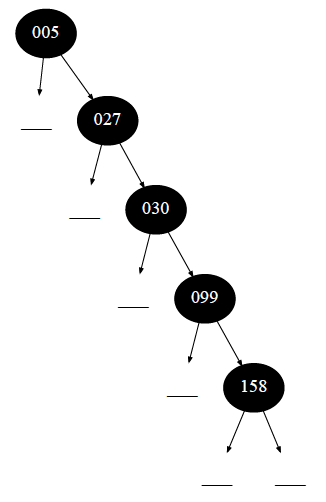
Рисунок — двоичное дерево поиска, вырожденное в линейный список.
Что касается вычислительной сложности представленного алгоритма, то, очевидно, что она составляет $O( n )$, где $n$ — количество вершин в заданном дереве.
Другими словами, чтобы найти все полные узлы, необходимо один раз проверить каждую вершину двоичного дерева поиска. В моей реализации обход дерева реализован рекурсивно.
➡ Пишите в комментариях, что непонятно в рамках приведенного алгоритма, а также насколько часто на практике вам приходилось сталкиваться с нахождением полных узлов заданного бинарного поискового дерева.
| ВНИМАНИЕ | Для заказа программы на бинарное дерево поиска пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий