Иногда мне приходится проверять заданное двоичное дерево на то, что оно является поисковым деревом. То есть нужно четко понимать разницу между простым двоичным деревом и двоичным деревом поиска. Это не одно и то же!
На этом рисунке показано стандартное, ничем не примечательное бинарное поисковое дерево:
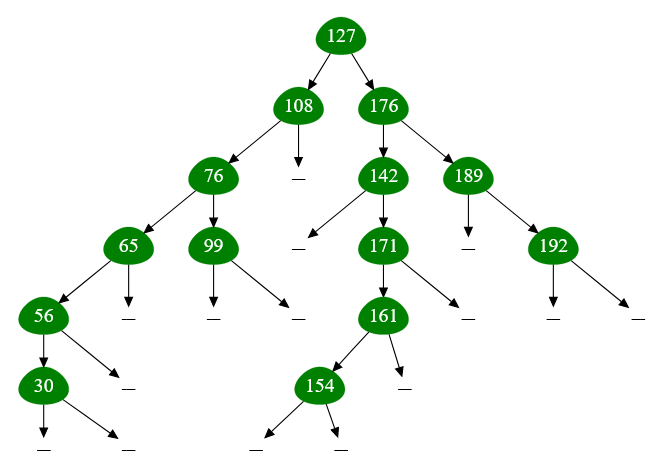
Рисунок — стандартное бинарное дерево поиска
А теперь я покажу просто двоичное дерево, которое не является поисковым, хотя структурно оно выглядит идентично поисковому двоичному дереву:
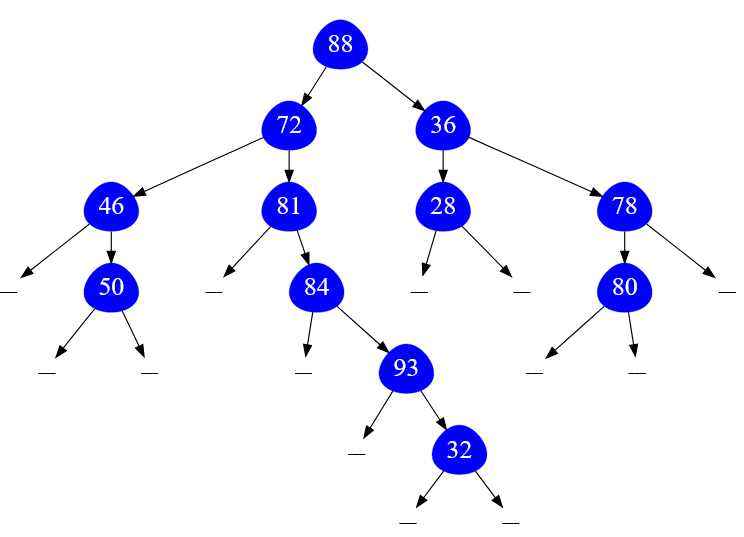
Рисунок — бинарное дерево ( не поиска )
💡 Почему это двоичное дерево не является деревом поиска? Потому что для ряда узлов не выполняются главные свойства дерева поиска:
для всех узлов левого ( правого ) поддерева произвольного взятого узла значения ключей должны быть меньше ( больше ), чем значения ключа самого этого узла
Покажу на рисунке, для каких узлов не выполняются главные требования к ключам поискового двоичного дерева:
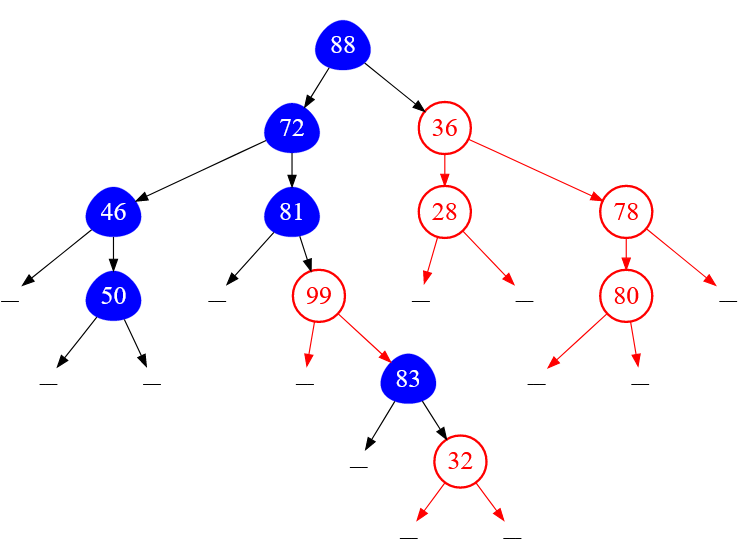
Рисунок — выделенные ( красные ) узлы нарушают «поисковость» двоичного дерева
➡ Например, чем не угодил узел с ключом $32$? Дело в том, что эта вершина является правым сыном родительской вершины с ключом $83$, а правые сыновья должны иметь значение ключа больше родительского, а не меньше.
➡ А чем не угодил узел с ключом $99$? Прямым родителем этого узла является узел с ключом $81$. Пока все в порядке, так как правый сын имеет значение ключа больше родительского. Но косвенным родителем вершины с ключом $99$ также является и вершина ( кстати, эта вершина является корневой в данном двоичном дереве ) с ключом $88$. Значение $99$ больше, чем $88$, поэтому анализируемый узел с ключом $99$ должен оказаться в правом поддереве относительно вершины с ключом $88$, а по факту оказался в левом поддереве — ошибка.
➡ А что не так с целой группой вершин, имеющих ключи $28$, $36$, $78$, $80$? Дело в том, что все эти значения меньше, чем $88$, поэтому все эти вершины в бинарном дереве поиска оказались бы в левом поддереве относительно вершины с ключом $88$, а не в правом.
Я хочу запрограммировать на языке «чистый» Си функцию, которая бы проверяла заданное бинарное дерево на бинарное поисковое дерево! Это сделать сложнее, чем кажется с первого взгляда. Существует достаточно много алгоритмов этой идеи. Я предлагаю, как мне кажется, один из эффективнейших способов такой проверки.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
//------------------------------------------------------------------------------ // 0 - проверяемое дерево не является бинарным деревом поиска // 1 - проверяемое дерево является бинарным деревом поиска // node - указатель на текущий узел двоичного дерева // min_key - минимальное значение ключа для текущего узла // max_key - максимальное значение ключа для текущего узла //------------------------------------------------------------------------------ int Is_bst( const Node* const node, const int min_key, const int max_key ) { if ( node == NULL ) { return 1; } if ( ( min_key < node -> key ) and ( node -> key < max_key ) ) { return ( Is_bst( node -> left, min_key, node -> key ) and Is_bst( node -> right, node -> key, max_key ) ); } return 0; } //------------------------------------------------------------------------------ |
При первом вызове этой рекурсивно-каскадной функции Is_bst() следует передать указатель на корень проверяемого двоичного дерева, а также границы ключей. В языке Си есть встроенные целочисленные лимитные константы, поэтому в своих программах эту функцию я вызываю так:
|
1 |
int is_bst = Is_bst( root, INT_MIN, INT_MAX ); |
Пишите в комментариях, что непонятно по проверке двоичного дерева на «поисковость». Расскажите, какие алгоритмы проверки применяли на практике вы, а также оцените вычислительную сложность этих алгоритмов.
| ВНИМАНИЕ | Для заказа программы на бинарное дерево поиска пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий