Есть такое понятие «level order traversal of binary tree». Это ничто иное, как поуровневый обход ( вывод ) двоичного дерева. Периодически на практике я сталкиваюсь с такой задачей, поэтому решил сделать шпаргалку-заметку, как это реализовать на языке программирования. Также расскажу более подробно об этом алгоритме.
Для анализа мне потребуется стандартное бинарное дерево, необязательно оно должно быть поисковым, но я буду исследовать алгоритм именно на двоичном дереве поиска. Например, на этом:
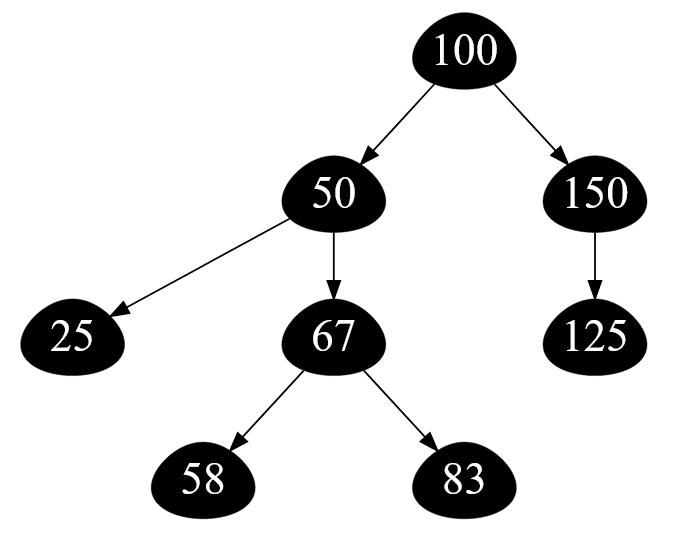
Рисунок — классическое двоичное дерево поиска ( ключи узлов — натуральные числа )
Давайте сразу договоримся, что корень дерева ( узел с ключом $100$ ) лежит на уровне $\#1$. В теории алгоритмов многие считают корневой уровень равный $0$. В принципе, это абсолютно не важно, но я выбирают счет от $1$!
Сейчас я приведу картинку с тем же самым двоичным деревом, но его узлы, принадлежащие разным уровням, будут закрашены в разные цвета.
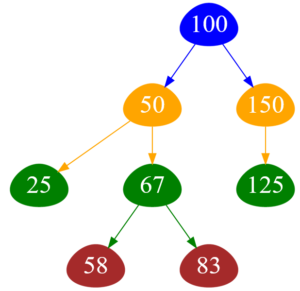
Рисунок — бинарное дерево с поуровневой раскраской узлов
Поуровневый обход такого дерева должен давать примерно такие результаты ( например, вывод на экран пользователю ):
| Уровень | Ключи | Цвет |
| $1$ | $100$ | синий |
| $2$ | $50,\ 150$ | оранжевый |
| $3$ | $25,\ 67,\ 125$ | зеленый |
| $4$ | $58,\ 83$ | коричневый |
➡ Вспомогательная операция — когда по запросу пользователя выводятся узлы заданного уровня. Но это реализуется достаточно тривиально, если есть готовая функция горизонтального обхода бинарного дерева.
Сейчас надо подумать, насколько сложно реализовать поуровневый обход двоичного дерева. В одной из своих заметок-шпаргалок я показывал, какие бывают классические типы обходов бинарного дерева. Всего было продемонстрировано $6$ рекурсивных обходов, причем все они работали «на глубину», то есть при обходе дерева алгоритм стремился спускаться по ветвям. При горизонтальном обходе узлов дерева нужен другой подход!
💡 Думаю, что придется отказаться от рекурсивной функции, которая посещает все вершины двоичного дерева по горизонтальным слоям, и воспользоваться итеративным подходом.
Тем, кто знаком с теорией графов, наверняка приходит на ум алгоритм BFS ( Breadth-first-search, обход в ширину ). Да, это верная идея. Именно этот алгоритм я попробую адаптировать для послойного обхода узлов двоичного дерева.
➡ Как известно, алгоритм BFS задействуют такую популярную структуру данных, как очередь. Поэтому для начала мне придется запрограммировать все базовые операции над очередью.
Для начала задекларирую типы данных, описывающих элементы очереди, а также саму очередь:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
//--------------------------------------------------------------------------- // описание сущности [Элемент очереди] //--------------------------------------------------------------------------- typedef struct Elem { Node* node; // указатель на узел двоичного дерева struct Elem* next; // указатель на следующий элемент очереди } Elem; //--------------------------------------------------------------------------- // описание сущности "Очередь" ( очередь - контейнер для ее элементов ) //--------------------------------------------------------------------------- typedef struct Queue { Elem* begin; // указатель на начало очереди ( на 1-ый элемент ) Elem* end; // указатель на конец очереди ( на n-ый элемет ) int size; // размер ( текущее количество элементов очереди ) } Queue; //--------------------------------------------------------------------------- |
А вот прототипы функций, для работы с очередью и ее элементами:
|
1 2 3 4 5 6 7 8 9 10 |
//--------------------------------------------------------------------------- // прототипы функций для работы с очередью и ее элементами //--------------------------------------------------------------------------- void Init( Queue* const ); Elem* Create_elem( Node* const ); int Empty( const Queue* const ); Elem* Front( const Queue* const ); void Pop( Queue* const ); void Push( Queue* const, Node* const ); //--------------------------------------------------------------------------- |
Приводить полный код функций для работы с очередью не буду ( оставляю вам на откуп их несложную реализацию ), но словесно поясню назначение каждой функции:
| # | Функция | Назначение |
| $1$ | void Init( Queue* const ); | Инициализация очереди перед началом работы. |
| $2$ | Elem* Create_elem( Node* const ); | Создание элемента очереди перед тем, как он будет добавлен в конец очереди. |
| $3$ | int Empty( const Queue* const ); | Проверка очереди на пустоту ( 0 — непустая; 1 — пустая ). |
| $4$ | Elem* Front( const Queue* const ); | Получение указателя на первый элемент очереди. При этом сам элемент из очереди не удаляется. |
| $5$ | void Pop( Queue* const ); | Физическое удаление элемента из конца очереди. |
| $6$ | void Push( Queue* const, Node* const ); | Добавление нового элемента в конец очереди. |
💡 Основная идея поуровневого обхода вершин двоичного дерева в следующем: в одну из очередей помещаются вершины текущего слоя дерева, а во вторую очередь помещаются сыновья всех вершин из первой очереди. В процессе работы алгоритма вторая очередь замещают первую.
➡ Очень важно понимать, что элементом очереди является указатель на вершину двоичного дерева ( это поле Node* node в структуре Elem ).
На старте алгоритма в первую очередь помещается элемент, указывающий на корень дерева, а вторая очередь является пустой:
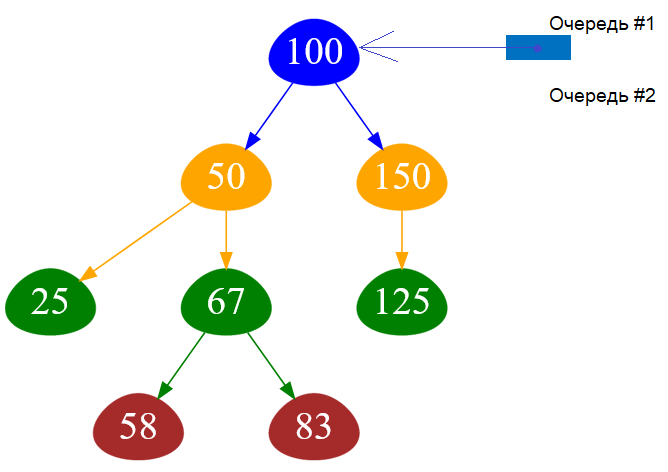
Рисунок — старт алгоритма горизонтального обхода двоичного дерева
Затем в цикле получаем все элементы из очереди #1 и в очередь #2 добавляем соответствующие вершины-сыновья полученных элементов:
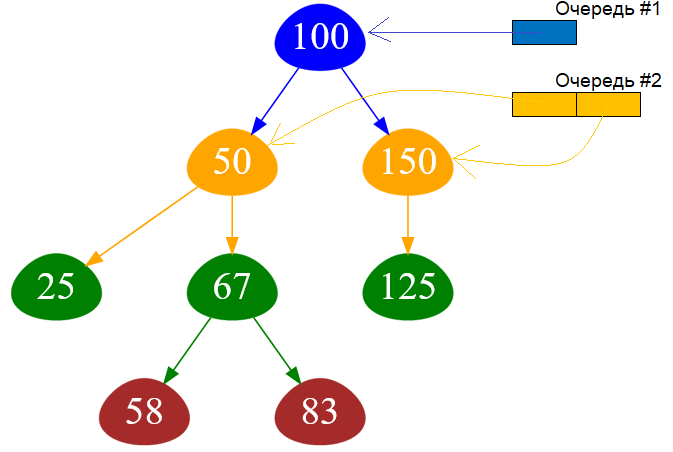
Рисунок — добавление вершин-сыновей в очередь #2
Обработанные элементы очереди #1 удаляются из нее и, когда очередь #1 становится пустой, то происходит замещение очереди #1 очередью #2:
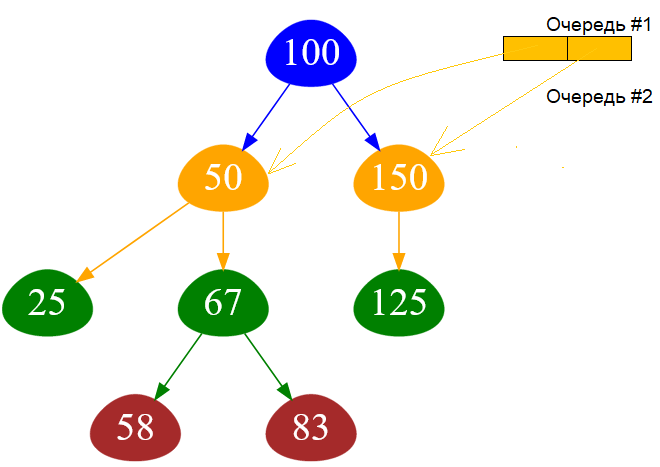
Рисунок — очередь #2 замещает очередь #1
➡ Этот процесс продолжается до тех пор, пока обе очереди не станут пустыми.
Очевидно, что в процессе работы алгоритма происходит также выпечатывание на экран ( или файл ) значения ключей вершин двоичного дерева.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
//------------------------------------------------------------------------------ // поуровневый ( послойный, горизонтальный ) обход бинарного дерева // node - указатель на корень двоичного дерева //------------------------------------------------------------------------------ void Levels_order( Node* const node ) { // хранит указатели на узлы двоичного дерева текущего ( родительского ) уровня Queue current_level_queue; // хранит указатели на узлы двоичного дерева следущего ( дочернего ) уровня Queue next_level_queue; // отвечает за #уровня int level; // стартовая инициализация обоих очередей Init( ¤t_level_queue ); Init( &next_level_queue ); level = 1; // на случай, если на обработку подается пустое двоичное дерево if ( node == NULL ) { return; } // в очередь #1 добавляем указатель на корень дерева Push( ¤t_level_queue, node ); printf( "Уровень #%2d", level ); // пока не все узлы заданного двоичного дерева просмотрены while ( 1 ) { // получаем указатель на первый элемент очереди #1 Elem* current_elem = Front( ¤t_level_queue ); Node* current_node = current_elem -> node; // выводим на экран значения ключа текущего узла printf( "%6d", current_node -> key ); // добавляем в очередь #2 всех сыновей родительского текущего узла if ( current_node -> left != NULL ) { Push( &next_level_queue, current_node -> left ); } if ( current_node -> right != NULL ) { Push( &next_level_queue, current_node -> right ); } // удаляем из очереди #1 элемент, т к соответствущая вершина дерева была обработана Pop( ¤t_level_queue ); // если все элементы очереди #1 обработаны и она стала пустой, то if ( Empty( ¤t_level_queue ) ) { // если в "дочерней" очереди нет элементов, то конец всей обработке if ( Empty( &next_level_queue ) ) { break; } // происходит замещение очереди #1 очередью #2 printf( "\n" ); current_level_queue = next_level_queue; Init( &next_level_queue ); // вывод на экран информации о номере уровня level++; printf( "Уровень #%2d", level ); } } } |
Моя программа для представленного выше двоичного дерева ( поиска ) выдает следующие результаты:
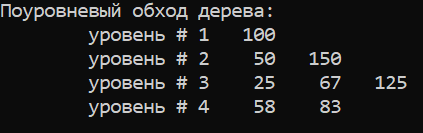
Рисунок — результаты работы программы
Также хочу прогнать функцию для более «ветвистого» двоичного дерева ( поиска ), например, для такого:
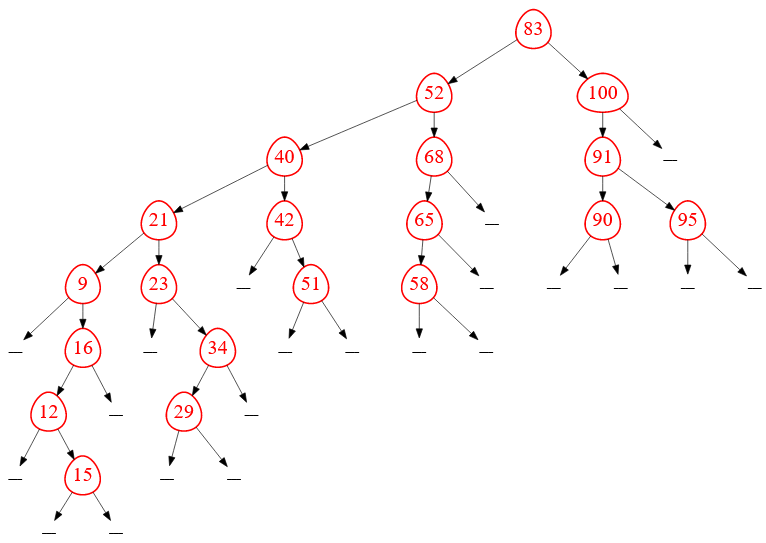
Рисунок — более «ветвистое» двоичное дерево ( поиска ) для теста
Результаты получились следующими:
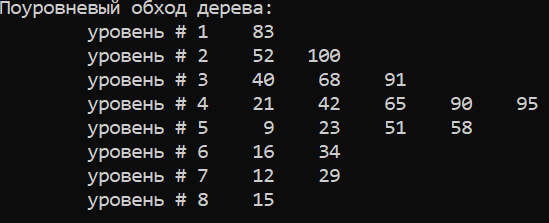
Рисунок — результаты работы программы для «ветвистого» двоичного дерева ( поиска )
💡 Хочу отметить такой момент: в своей программной реализации для послойного обхода вершин двоичного дерева я задействовал $2$ очереди:
| ➡ | первая очередь отвечала за вершины бинарного дерева, находящиеся на «текущем» уровне; |
| ➡ | вторая ( вспомогательная ) очередь отвечала за вершины бинарного дерева, находящиеся на «следующем» уровне. |
Зачастую проуровневый обход дерева кодируют с применением лишь одной очереди. Но это дело вкуса. Мне удобнее было задействовать две очереди.
Также существуют рекурсивные алгоритмы горизонтального обхода узлов бинарного дерева ( поиска ), но они сложны для понимания и их крайне неудобно программировать.
➡ Пишите в комментариях, что непонятно в рамках рассказанного алгоритма поуровневого вывода двоичного дерева, а также в каких случаях на практике вам приходилось столкнуться с этим алгоритмом.
| ВНИМАНИЕ | Для заказа программы на двоичное дерево ( поиска ) пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий