Сразу замечу, что дерево необязательно должно быть поисковым, но обязательно должно быть бинарным. Также симметричность я буду проверять с точки зрения связей вершин дерева, а не значений ключей.
Почему я не исследую проверку на зеркальность с точки зрения ключевых значений? Да потому что, если дерево является поисковым, то «ключевая» зеркальность в таком дереве в принципе невозможна. Поэтому все изображения деревьев, которые буду приводить в данной статье-шпаргалке, не будут иметь никаких значений, то есть я буду показывать все алгоритмы на анонимных бинарных деревьях.
Для начала было бы неплохо понять, какое двоичное дерево является симметричным, а какое — нет. Вот $2$ картинки.

Рисунок — несимметричное ( относительно корня ) двоичное дерево
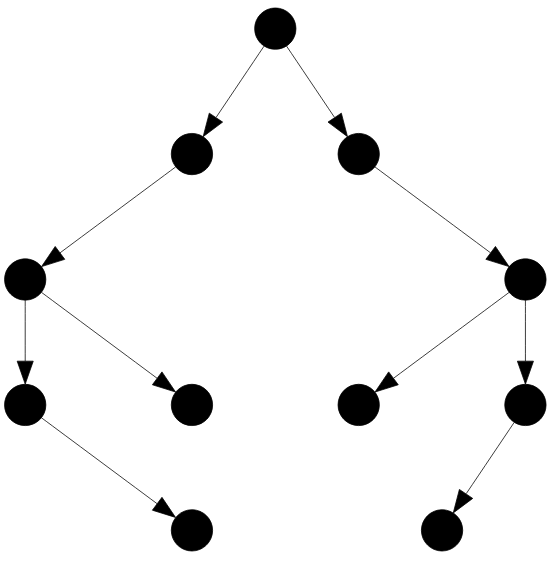
Рисунок — симметричное ( относительно корня ) двоичное дерево
Если двоичное дерево можно разделить плоскостью на два поддерева так, чтобы узлы одной половины, отразившись в этой плоскости ( как в зеркале ), повторили узлы другой половины, то можно говорить, что рассматриваемое бинарное дерево обладает зеркальной симметрией.
💡 Очевидно, что виртуальная плоскость проходит через вершину двоичного дерева.
На следующем рисунке показана плоскость, проходящая через вершину двоичного дерева, а симметрично-зеркальные узлы раскрашены в соответственные цвета.
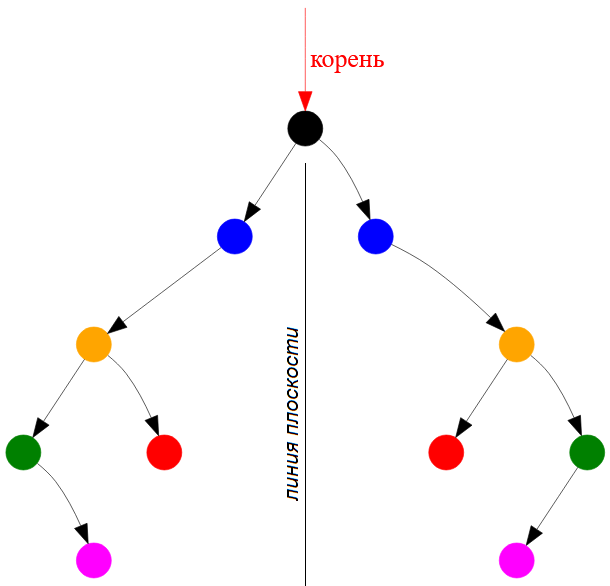
Рисунок — два бинарных поддерева, разделенных зеркальной плоскостью
Моя конечная цель — написание программной функции, которая проверяет заданное двоичное дерево на зеркальную симметрию относительно корня.
➡ Очевидно, что мне придется рекурсивно перебирать узлы дерева и отслеживать направления «спуска». Но перебирать узлы нужно одновременно в обоих поддеревьях. Следовательно, мне нужно иметь $2$ поддерева при проверке, поэтому функция на вход будет принимать $2$ указателя: указатель на корень левого поддерева и указатель на корень правого поддерева.
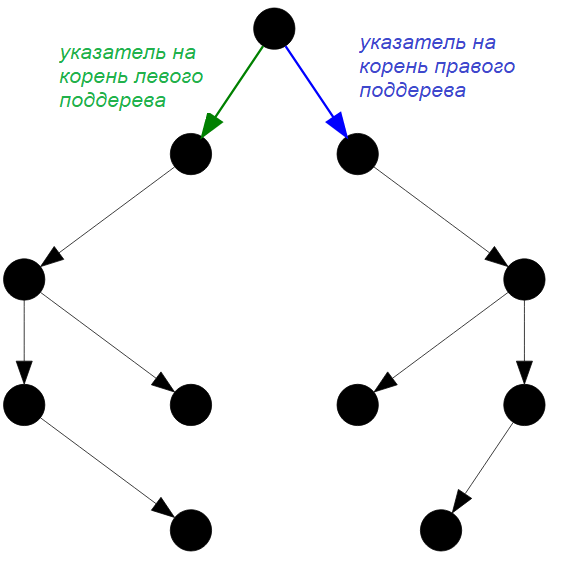
Рисунок — при проверке на симметричность надо иметь указатели на левое и правое бинарное поддерево
💡 Если количество вершин в заданном двоичном дереве поиска — четное число ( например, $12$ ), то гарантировано это бинарное дерево не является зеркально-симметричным. Один узел будет корневым и остается $11$ узлов, которые нужно в равной пропорции разделить на два поддерева. Математически это невозможно!
В общем не стоит предварительно рассчитывать количество узлов в заданном дереве, так как эта операция имеет вычислительную сложность $O( n )$, $n$ — количество вершин.
➡ Нужно понимать такой момент ( правило ): если количество NULL-касаний в левом и правом поддереве равно и зеркально соответственно друг другу, то проверяемое бинарное дерево является зеркально-симметричным относительно своего корня.
На следующем рисунке показаны $2$ зеркально-симметричных NULL-касания.
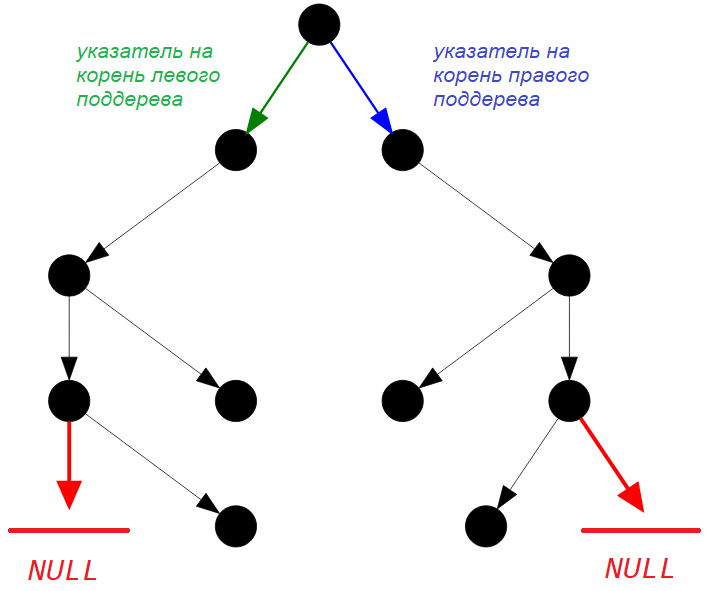
Рисунок — два зеркально-симметричных NULL-касания
В результате всех приведенных размышлений закодировал следующую функцию ( разумеется, рекурсивную, так как бинарные деревья крайне удобно обрабатывать рекурсивно ) на языке «чистый» Си:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
//------------------------------------------------------------------------------ // проверка бинарного дерева на зеркальную симметрию относительно корня // left_node - указатель на левое поддерево, проверяемого бинарного дерева // right_node - указатель на правое поддерево, проверяемого бинарного дерева // в качестве результата возвращается целое число: // 0 - проверяемое двоичное дерево не является зеркально-симметричным // 1 - проверяемое двоичное дерево является зеркально-симметричным //------------------------------------------------------------------------------ int Is_mirrow_simmetric( const Node* const left_node, const Node* const right_node ) { // если какой-либо из узлов поддеревьев нулевой, то конец рекурсивных вызовов if ( ( left_node == NULL ) or ( right_node == NULL ) ) { // узел из другого поддерева также должен быть нулевым return ( ( left_node == NULL ) and ( right_node == NULL ) ); } // каскадная рекурсия, которая симметрично обходит узла проверяемого дерева // если в левом поддереве шаг влево, то в правом, соответственно, шаг право // если в левом поддереве шаг вправо, то в правом, соответственно, шаг влево return Is_mirrow_simmetric( left_node -> left, right_node -> right ) and Is_mirrow_simmetric( left_node -> right, right_node -> left ); } //------------------------------------------------------------------------------ |
Вызов этой функции может иметь такой вид:
|
1 2 |
// root - указатель на корень проверяемого на зеркальную симметричность двоичного дерева printf( "\n\nЗеркальная симметрия ( 0 - НЕТ; 1 - ДА ): %d", Is_mirrow_simmetric( root -> left, root -> right ) ); |
Из представленной программной реализации видно, что вершины левого поддерева я посещаю LKP-обходом, а правого — PKL-обходом. Напомню, что всего существует $6$ классических способов обхода двоичного дерева ( поиска ).
Что касается вычислительной сложности функции Is_mirrow_simmetric(). Очевидно, что в «худшем» случае нужно посетить все вершины проверяемого на симметричность двоичного дерева. Но их достаточно посетить только по $1$ разу. Следовательно, вычислительная сложность приведенного алгоритма составляет $O( n )$, где $n$ — количество вершин проверяемого бинарного дерева.
💡 Но быстродействие функции Is_mirrow_simmetric() в некоторых случаях можно увеличить, если обратить внимание на следующий нюанс. Иногда можно выяснить, что проверяемое бинарное дерево не является зеркально-симметричным, даже не достигнув NULL-касания. Рассмотрим следующее дерево.
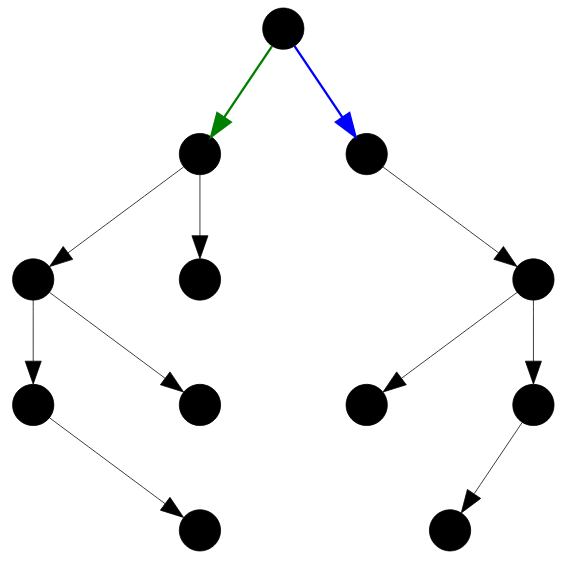
Рисунок — почти зеркально-симметричное двоичное дерево
Симметричность этого дерева нарушается на элементах, выделенных красным цветом ( см. рисунок ниже ), но алгоритм продолжает проверки, так как никакого NULL-касания достигнуто не было. Следовательно, можно прерывать обработку, если статусы текущих вершин дерева зеркально не соответственны друг другу.
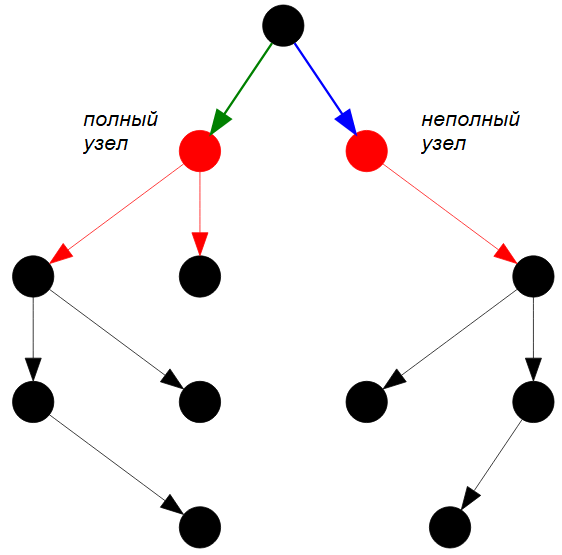
Рисунок — нарушение зеркальной симметрии на красных узлах
➡ Пишите в комментариях, что непонятно в рамках рассмотренного алгоритма, который проверяет заданное двоичное дерево ( поиска ) на зеркальную симметричность относительного своего корня. Если знаете принципиально другие подходы к такой проверке дерева, то расскажите о них в комментариях.
| ВНИМАНИЕ | Для заказа программы на бинарное дерево ( поиска ) пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий